浙江省湖州市长兴县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-08-09 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分)

1. 要使分式 $\frac{1}{x}$ 有意义，x的取值范围满足（）

A、x≠0 B、x=0 C、x＞0 D、x＜0

查看试题解析
2. 下列计算中，正确的是（）

A、a³+a²=a⁵ B、(2a)³=6a³ C、a⁵÷a²=a³ D、(a+1)²=a²+1

查看试题解析
3. 已知 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 是关于x，y的二元一次方程x-ay=3的一个解，则a的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
4. 如图，∠B的同位角可以是（）

A、∠1 B、∠2 C、∠3 D、∠4

查看试题解析
5. 计算2a³b·(-3b²c)÷(4ab³)，所得的结果是（）

A、 $- \frac{3}{2}$ a²bc B、 $- \frac{2}{3}$ a²c C、 $\frac{3}{2}$ ac D、 $- \frac{3}{2}$ a²c

查看试题解析
6. 如图，小慧从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，此时需要将方向调整到与出发时一致，则方向的调整应为（）

A、左转80° B、右转80° C、左转100° D、右转100°

查看试题解析
7. 下列各式因式分解正确的是（）

A、2x²-4xy+9y²=(2x-3y)² B、x(x-y)+y(y-x)=(x-y)(x+y) C、2x²-8y²=2(x-4y)(x+4y) D、x²+6xy+9y²=(x+3y)²

查看试题解析
8. 如图，直线l∥m∥n，三角形ABC的顶点B，C分别在直线n和m上，边BC与直线n所夹的角为25°，且∠ACB=60°，则∠a的度数为（）

A、25° B、30° C、35° D、45°

查看试题解析
9. 随着电影《流浪地球》的热映，其同名科幻小说的销量也急剧上升．某书店分别用600元和900元两次购进该小说，第二次数量比第一次多50套，且两次进价相同．若设该书店第一次购进x套，由题意列方程正确的是（）

A、 $\frac{600}{x} = \frac{900}{x - 50}$ B、 $\frac{600}{x - 50} = \frac{900}{x}$ C、 $\frac{600}{x} = \frac{900}{x + 50}$ D、 $\frac{600}{x + 50} = \frac{900}{x}$

查看试题解析
10. 在长方形ABCD内，将两张边长分别为a和b(a>b)的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，设图1中未被这两张正方形纸片覆盖的面积为S₁ ，图2中未被这两张正方形纸片覆盖的面积为S₂ ，当S₂-S₁=b时，AD-AB的值为（）

A、1 B、2 C、2a-2b D、b

查看试题解析

二、填空题(本题有6小题，每小题2分，共12分)

11. 用科学记数法表示：0.00000136=。

查看试题解析
12. 若a+b=2，ab=1，则a²b+ab²= 。

查看试题解析
13. 某校701班数学期终考试全班所有学生成绩的频数分布直方图如图所示，满分100分，学生成绩取整数，则成绩在90.5~95.5这一分数段的频率是。

查看试题解析
14. 当x=时，分式 $\frac{| x | - 3}{x - 3}$ 的值为零。

查看试题解析
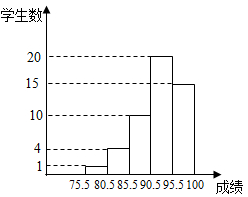15. 若(x+2019)（x+2018)=1009，则(x+2019)²+(x+2018)²=。

查看试题解析
16. 数学家发明了一个魔术盒，当任意数对(a，b)进入其中时，会得到一个新的数(a-2)(b-1)．现将数对(1，m)放入其中，得到数n，再将数对(n，m)放入其中后，最后得到的数是．(结果用含m的代数式表示)

查看试题解析

三、解答题(本题共有8小题，共58分)

17. 因式分解：

(1)、x²-4

(2)、a³b-2a²b+ab

查看试题解析
18. 先化简，再求值：(a-1)(a+1)-(a-2)² ，其中a= $\frac{1}{4}$

查看试题解析
19. 解方程(组)：

(1)、 ${\begin{cases} 2 x + 7 y = 5 \\ 3 x + y = - 2 \end{cases}$

(2)、 $\frac{2 x + 5}{x - 3} = \frac{1}{2}$

查看试题解析
20. 如图，直线AB∥CD，BC平分∠ABD，∠1=50°，求∠2的度数。

查看试题解析
21. 某县特色早餐种类繁多，色香味美，著名的种类有“干挑面”、“锅贴”、“青团子” “粢米饭”等。一数学兴趣小组在全校范围内随机抽取了一些同学进行“我最喜爱的特色早餐”调查活动，每位同学选择一种自己最喜欢的早餐种类，将调查结果绘制成如下两幅不完整的统计图．请根据图中的信息，解答下列问题：

(1)、请将条形统计图补充完整。

(2)、在扇形统计图中，表示“粢米饭”对应的扇形的圆心角是多少度?

(3)、该校共有1200名学生，请你估计该校学生中最喜爱“青团子”的学生有多少人?

查看试题解析
22. 阅读材料：小丁同学在解方程组 ${\begin{cases} \frac{x + y}{3} + \frac{x - y}{5} = 4 \\ \frac{x + y}{3} - \frac{x - y}{5} = - 2 \end{cases}$ 时，他发现：如果直接用代入消元法或加减消元法求解运算量比较大，也容易出错．如果把方程组中的(x+y)看作一个整体，把(x-y)看作一个整体，通过换元，可以解决问题．以下是他的解题过程：
设m=x+y，n=x-y，这时原方程组化为 ${\begin{cases} \frac{m}{3} + \frac{n}{5} = 4 \\ \frac{m}{3} - \frac{n}{5} = - 2 \end{cases}$

解得 ${\begin{cases} m = 3 \\ n = 15 \end{cases}$ ，即 ${\begin{cases} x + y = 3 \\ x - y = 15 \end{cases}$ ，解得 ${\begin{cases} x = 9 \\ y = - 6 \end{cases}$

请你参考小丁同学的做法，解方程组： ${\begin{cases} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{cases}$

查看试题解析
23. 某市为创建生态文明城市，对公路旁的绿化带进行全面改造．现有甲、乙两个工程队，有三种施工方案：
方案一：甲队单独完成这项工程，刚好能如期完成；

方案二：乙队单独完成这项工程，要比预定工期多用3天；

方案三：先由甲、乙两队一起合作2天，剩下的工程由乙队单独完成，刚好如期完成。

(1)、求工程预定工期的天数

(2)、若甲队每施工一天需工程款2万元，乙队每施工一天需工程款1.3万元．为节省工程款，同时又如期完工，请你选择一种方案，并说明理由

查看试题解析
24. 如图1，直线MN与直线AB，CD分别交于点E，F，∠1与∠2互补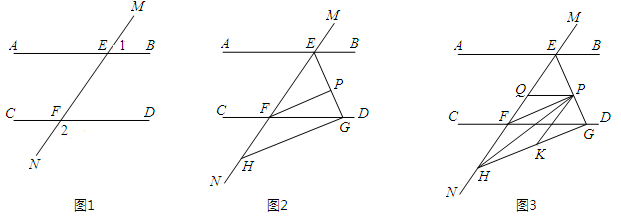

(1)、试判断直线AB与直线CD的位置关系，并说明理由

(2)、如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH

(3)、如图3，在(2)的条件下，连结PH，在GH上取一点K，使得∠PKG=2∠HPK，过点P作PQ平分∠EPK交EF于点Q，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．(温馨提示：三角形的三个内角和为180°．)

查看试题解析