浙江省温岭市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2019-08-09 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题4分，共40分)

1. 下列代数式中，属于最简二次根式的是（）

A、 $\sqrt{7}$ B、 $\sqrt{\frac{2}{3}}$ C、 $\sqrt{12}$ D、 $\sqrt{0.5}$

查看试题解析
2. 在▱ABCD中，∠A、∠B的度数之比为5：4，则∠C等于（）

A、60° B、80° C、100° D、120°

查看试题解析
3. 若一元二次方程ax²+bx+c=0(a≠0)有一个根为-1，则a-b+c的值是（）

A、-1 B、1 C、0 D、不能确定

查看试题解析
4. 下列变量之间关系中，一个变量是另一个变量的正比例函数的是（）

A、正方形的面积S随着边长x的变化而变化 B、正方形的周长C随着边长x的变化而变化 C、水箱有水10升，以0.5升/分的流量往外放水，剩水量(升)随着放水时间t(分)的变化而变化 D、面积为20的三角形的一边a随着这边上的高h的变化而变化

查看试题解析
5. 下列给出的条件中不能判定一个四边形是矩形的是（）

A、一组对边平行且相等，一个角是直角 B、对角线互相平分且相等 C、有三个角是直角 D、一组对边平行，另一组对边相等，且对角线相等

查看试题解析
6. 在某学校汉字听写大赛中，有21名同学参加比赛，预赛成绩各不相同，要取前10名才能参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需要再知道这21名同学成绩的（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
7. 关于 $\frac{\sqrt{5} - 1}{2}$ ，下列说法错误的是（）

A、它是无理数 B、它是方程x²+x-1=0的一个根 C、0.5< $\frac{\sqrt{5} - 1}{2}$ ＜1 D、不存在实数，使x²= $\frac{\sqrt{5} - 1}{2}$

查看试题解析
8. 五一小长假，李军与张明相约去宁波旅游，李军从温岭北上沿海高速，同时张明从玉环芦浦上沿海高速，温岭北与玉环芦浦相距44千米，两人约好在三门服务区集合，李军由于离三门近，行驶了1.2小时先到达三门服务站等候张明，张明走了1.4小时到达三门服务站。在整个过程中，两人均保持各自的速度匀速行驶，两人相距的路程y千米与张明行驶的时间x小时的关系如图所示，下列说法错误的是（）

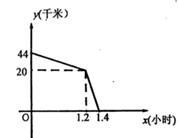A、李军的速度是80千米/小时 B、张明的速度是100千米/小时 C、玉环芦浦至三门服务站的路程是140千米 D、温岭北至三门服务站的路程是44千米

查看试题解析
9. 定义：在同一平面内画两条相交、有公共原点的数轴x轴和y轴，交角a≠90°，这样就在平面上建立了一个斜角坐标系，其中w叫做坐标角，对于坐标平面内任意一点P，过P作y轴和x轴的平行线，与x轴、y轴相交的点的坐标分别是a和b，则称点P的斜角坐标为(a，b)．如图，w=60°，点P的斜角坐标是(1，2)，过点P作x轴和y轴的垂线，垂足分别为M、N，则四边形OMPN的面积是（）

A、 $\frac{13 \sqrt{3}}{6}$ B、 $\frac{13 \sqrt{3}}{8}$ C、 $\frac{1 + 2 \sqrt{3}}{2}$ D、3

查看试题解析
10. 如图，E，F分别是正方形ABCD边AD、BC上的两定点，M是线段EF上的一点，过M的直线与正方形ABCD的边交于点P和点H，且PH=EF，则满足条件的直线PH最多有（）条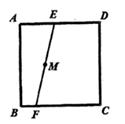

A、1 B、2 C、3 D、4

查看试题解析

二、填空题(木题有6小题，每小题5分，共30分)

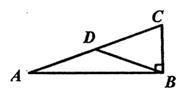
11. 要使二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是。

查看试题解析
12. 一元二次方程x²-2x-k=0有两个相等的实数根，则k=。

查看试题解析
13. 如图，在R△ABC中，∠ABC=90°，AB=2 $\sqrt{2}$ ，BC=1，BD是AC边上的中线，则BD= 。

查看试题解析
14. 若八个数据x₁ ， x₂ ， x₃_{， ……}x₈ ，的平均数为8，方差为1，增加一个数据8后所得的九个数据x₁ ， x₂ ， x₃ ， …x₈；8的平均数 $\bar{x}$ 8，方差为S₂ 1．(填“>”、“=”、“<”)

查看试题解析
15. 若已知方程组 ${\begin{cases} y = k x - b \\ y = - x + a \end{cases}$ 的解是 ${\begin{cases} x = - 1 \\ y = 3 \end{cases}$ ，则直线y=-kx+b与直线y=x-a的交点坐标是。

查看试题解析
16. 已知，四边形ABCD中，AB∥CD，AB=8，DC=4，点M、N分别为边AB、DC的中点，点P从点D出发，以每秒1个单位的速度从D→C方向运动，到达点C后停止运动，同时点Q从点B出发，以每秒3个单位的速度从B→A方向运动，到达点A后立即原路返回，点P到达点C后点Q同时停止运动，设点P、Q运动的时间为t秒，当以点M、N、P、Q为顶点的四边形为平行四边形时，t的值为。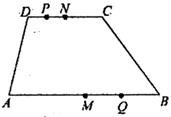

查看试题解析

三、解答题(第17~20题，每题8分，第21题10分，第22-23题，每题12分，第24题14分，共80分)

17. 计算：

(1)、 $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{32}$

(2)、 $\sqrt{6} \div \sqrt{2} + (\sqrt{3} + 2 \sqrt{2}) (\sqrt{3} - 2 \sqrt{2})$

查看试题解析
18. 解方程：

(1)、x²-4x=3

(2)、x²-4=2(x+2)

查看试题解析
19. 已知一次函数图象过点P(0，6)，且平行于直线y=-2x

(1)、求该一次函数的解析式

(2)、若点A( $\frac{1}{2}$ ，a)、B(2，b)在该函数图象上，试判断a、b的大小关系，并说明理由。

查看试题解析
20. 如图△ABC中，点D是边AB的中点，CE∥AB，且AB=2CE，连结BE、CD。

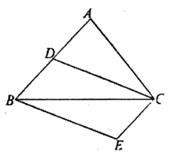(1)、求证：四边形BECD是平行四边形；

(2)、用无刻度的直尺画出△ABC边BC上的中线AG(保留画图痕迹)

查看试题解析

21. 王达和李力是八(2)班运动素质最好的两位同学，为了选出一名同学参加全校的体育运动大寒，班主任针对学校要测试的五个项目，对两位同学进行相应的测试(成绩：分)，结果如下：

姓名	力量	速度	耐力	柔韧	灵敏
王达	60	75	100	90	75
李力	70	90	80	80	80

根据以上测试结果解答下列问题：

(1)、补充完成下表：

姓名	平均成绩(分)	中位数(分)	众数(分)	方差(分²)
王达	80	75	75	190
李力

(2)、任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由；

(3)、若按力量：速度：耐力：柔韧：灵敏=1：2：3：3：1的比例折合成综合分数，推选得分同学参加比赛，请通过计算说明应推选哪位同学去参赛。

查看试题解析

22. 某蛋糕店为了吸引顾客，在A、B两种蛋糕中，轮流降低其中一种蛋糕价格，这样形成两种盈利模式，模式一：A种蛋糕利润每盒8元，B种蛋糕利润每盒15元；模式二：A种蛋糕利润每盒14元，B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒，且都能售完，设每天销售A种蛋糕x盒

(1)、设按模式一销售A、B两种蛋糕所获利润为y₁元，按模式二销售A、B两种蛋糕所获利润为y₂元，分别求出y₁、y₂关于x的函数解析式；

(2)、在同一个坐标系内分别画出(1)题中的两个函数的图象；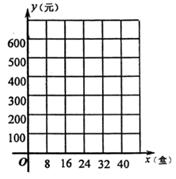

(3)、若y始终表示y₁、y₂中较大的值，请问y是否为x的函数，并说说你的理由，并直接写出y的最小值．

查看试题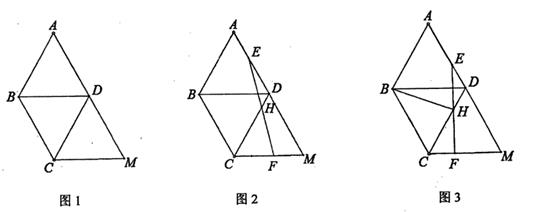解析
23. 如图

如图1，四边形ABCD和四边形BCMD都是菱形，

(1)、求证：∠M=60°

(2)、如图2，点E在边AD上，点F在边CM上，连接EF交CD于点H，若AE=MF，求证：EH=HF；

(3)、如图3，在第(2)小题的条件下，连接BH，若EF⊥CM，AB=3，求BH的长

查看试题解析
24. 小聪与小明在一张矩形台球桌ABCD边打台球，该球桌长AB=4m，宽AD=2m，点O、E分别为AB、CD的中点，以AB、OE所在的直线建立平面直角坐标系。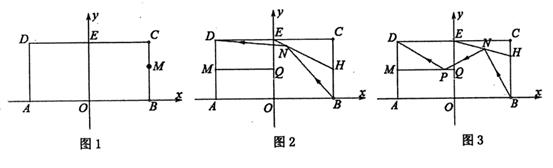

(1)、如图1，M为BC上一点；
①小明要将一球从点M击出射向边AB，经反弹落入D袋，请你画出AB上的反弹点F的位置；
②若将一球从点M(2，1.2)击出射向边AB上点F(0.5，0)，问该球反弹后能否撞到位于(-0.5，0.8)位置的另一球?请说明理由

(2)、如图2，在球桌上放置两个挡板(厚度不计)挡板MQ的端点M在AD中点上且MQ⊥AD，MQ=2m，挡板EH的端点H在边BC上滑动，且挡板EH经过DC的中点E；
①小聪把球从B点击出，后经挡板EH反弹后落入D袋，当H是BC中点时，试证明：DN=BN；

②如图3，小明把球从B点击出，依次经挡板EH和挡板MQ反弹一次后落入D袋，已知∠EHC=75°，请你直接写出球的运动路径BN+NP+PD的长。

查看试题解析