浙江省湖州市长兴县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-08-09 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 化简 的结果是( )A、-3 B、3 C、±3 D、92. 已知一组数据的方差是3,则这组数据的标准差是( )A、 B、3 C、 D、93. 关于反比例函数 , 下列说法中错误的是( )A、它的图象分布在一、三象限 B、它的图象过点(-1,-3) C、当x>0时,y的值随x的增大而增大 D、当x<0时,y的值随x的增大而减小4. 下列运算正确的是( )A、 + = B、 =2 C、 × = D、 ÷ =25. 关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k的值为( )A、k=4 B、k=-4 C、k≥-4 D、k≥46. 某县从2017年开始大力发展“竹文化”旅游产业.据统计,该县2017年“竹文化”旅游收入约为2亿元.预计2019年“竹文化”旅游收入达到2.88亿元,据此估计该县2018年,2019年“竹文化”旅游收入的年平均增长率约为( )A、2% B、20% C、4.4% D、44%7. 在△ABC中,AB=3,AC=4,BC=5,点P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )A、2.5 B、2.4 C、2.2 D、28. 如图,▱ABCD的周长为24,对角线AC,BD相交于点O,点E是CD的中点,BD=8,则△DOE的周长为( )
 A、6 B、8 C、10 D、149. 如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE折叠,使点B落在点F处,连结CF,当△CEF为直角三角形时,BE的长是( )
A、6 B、8 C、10 D、149. 如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE折叠,使点B落在点F处,连结CF,当△CEF为直角三角形时,BE的长是( ) A、4 B、3 C、4或8 D、3或610. 如图,点A,B在反比例函数y= (x<0)的图象上,连结OA,AB,以OA,AB为边作□OABC,若点C恰好落在反比例函数y= (x>0)的图象上,此时□OABC的面积是( )
A、4 B、3 C、4或8 D、3或610. 如图,点A,B在反比例函数y= (x<0)的图象上,连结OA,AB,以OA,AB为边作□OABC,若点C恰好落在反比例函数y= (x>0)的图象上,此时□OABC的面积是( )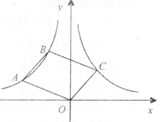 A、3 B、 C、 D、6
A、3 B、 C、 D、6二、填空题(本题有6小题,每小题4分,共24分)
-
11. 二次根式 中字母x的取值范围是12. 若4个数5,x,8,10的中位数为7,则x= 。13. 若关于x的一元二次方程(a-1)x2+ax+a2-1=0的一个根是0,则a的值是。14. 如图,河坝横断面迎水坡AB的坡比是1: (坡比是斜坡AB两点之间的高度差BC与水平距离AC之比),坝高BC=2m,则坡面AB的长度是m。
 15. 如图,在▱ABCD中,连结BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=5 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP= 。
15. 如图,在▱ABCD中,连结BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=5 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP= 。 16. 如图,已知反比例函数y= (x>0)的图象经过点A(4,5),若在该图象上有一点P,使得∠AOP=45°,则点P的坐标是 。
16. 如图,已知反比例函数y= (x>0)的图象经过点A(4,5),若在该图象上有一点P,使得∠AOP=45°,则点P的坐标是 。
三、解答题(本题共有8小题,共66分)
-
17. 计算:(1)、(2)、18. 解方程:(1)、2(x-3)=3x(x-3)(2)、x2-2x-1=019. 已知x与y成反比例,且当x= 时,y=(1)、求y关于x的函数表达式(2)、当x= 时,y的值是多少?20. 某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%,面试占40%计算候选人的综合成绩(满分为100分)
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)、这四名候选人面试成绩的中位数是。(2)、现得知候选人丙的综合成绩为87.6分,则表中x的值等于。(3)、求其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选。21. 如图,在▱ABCD中,点E,F分别在CD,BC延长线上,AE∥BD,EF⊥BF (1)、求证:四边形ABDE是平行四边形(2)、若∠ABC=60°,CF= ,求AB的长22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件。(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?23. 如图,已知A,F,C,D四点在同一条直线上,AF=CD,AB∥ED,且AB=ED。
(1)、求证:四边形ABDE是平行四边形(2)、若∠ABC=60°,CF= ,求AB的长22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件。(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?23. 如图,已知A,F,C,D四点在同一条直线上,AF=CD,AB∥ED,且AB=ED。 (1)、求证:△ABC≌△DEF。(2)、如果四边形EFBC是菱形,已知EF=3,DE=4,∠DEF=90°,求AF的长度。24. 如图,四边形ABCD的四个顶点分别在反比例函数y= 与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P,已知点B的横坐标为5。
(1)、求证:△ABC≌△DEF。(2)、如果四边形EFBC是菱形,已知EF=3,DE=4,∠DEF=90°,求AF的长度。24. 如图,四边形ABCD的四个顶点分别在反比例函数y= 与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P,已知点B的横坐标为5。 (1)、当m=10,n=30时
(1)、当m=10,n=30时①若点P的纵坐标为4,求直线AB的函数表达式
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由。
(2)、四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由。