初中数学浙教版八年级上册1.3 证明 同步训练
试卷更新日期:2019-08-09 类型:同步测试
一、证明
-
1. 下列图形中,由 ,能得到 的是( )A、
 B、
B、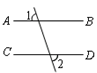 C、
C、 D、
D、 2. 下列叙述中,正确的有( )
2. 下列叙述中,正确的有( )①如果 ,那么 ;②满足条件 的n不存在;
③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;
④ΔABC中,若∠A+∠B=2∠C,∠A-∠C=40°,则这个△ABC为钝角三角形.
A、0个 B、1个 C、2个 D、3个3. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.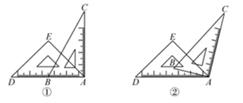 4. 在锐角三角形ABC中,AB>AC,AM为中线,P为△AMC内一点,证明:PB>PC(如图).
4. 在锐角三角形ABC中,AB>AC,AM为中线,P为△AMC内一点,证明:PB>PC(如图).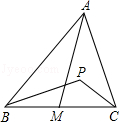 5. 某次体育比赛共有n(n≥3)名选手参加,每两名选手都比赛一局.现知无平局出现,而且每名选手都未能击败历有对手.求证:其中必存在3名选手甲、乙和丙,使得甲胜乙、乙胜丙、丙胜甲.
5. 某次体育比赛共有n(n≥3)名选手参加,每两名选手都比赛一局.现知无平局出现,而且每名选手都未能击败历有对手.求证:其中必存在3名选手甲、乙和丙,使得甲胜乙、乙胜丙、丙胜甲.
6. 动手操作,探究: (1)、探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
(1)、探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图(1),在△ADC中,DP,CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
(2)、探究二:若将△ADC改为任意四边形ABCD呢?已知:如图(2),在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.(写出说理过程)
(3)、探究三:若将上题中的四边形ABCD改为六边形ABCDEF(图(3))呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .二、三角形的外角
-
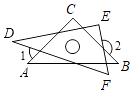
7. 如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC,∠ABC 之间存在的等量关系是( )
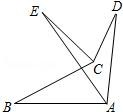 A、∠AEC=∠ABC﹣2∠ADC B、∠AEC= C、∠AEC= ∠ABC﹣∠ADC D、∠AEC=8. 如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=45°,∠DBC=105°,则∠C= .
A、∠AEC=∠ABC﹣2∠ADC B、∠AEC= C、∠AEC= ∠ABC﹣∠ADC D、∠AEC=8. 如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=45°,∠DBC=105°,则∠C= . 9. 如图,一副三角板的三个内角分别是90,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上).若固定△ABC,将△BDE绕着公共顶点B顺时针旋转a度(0<a<180),当边DE与△ABC的某一边平行时,相应的旋转角a的值为 。
9. 如图,一副三角板的三个内角分别是90,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上).若固定△ABC,将△BDE绕着公共顶点B顺时针旋转a度(0<a<180),当边DE与△ABC的某一边平行时,相应的旋转角a的值为 。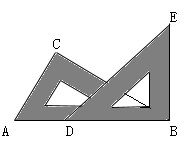 10. 如图,AF平分∠BAD,CF平分∠BCD的邻补角∠BCE,且AF与CF相交于点F,∠B=40°,∠D=20°,则∠F=°.
10. 如图,AF平分∠BAD,CF平分∠BCD的邻补角∠BCE,且AF与CF相交于点F,∠B=40°,∠D=20°,则∠F=°.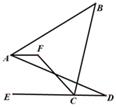 11. 生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
11. 生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的: (1)、图1中的∠ABC的度数为.(2)、图2中已知AE∥BC,则∠AFD的度数为.12. 中,三个内角的平分线交于点O,过点O作 ,交边AB于点D.
(1)、图1中的∠ABC的度数为.(2)、图2中已知AE∥BC,则∠AFD的度数为.12. 中,三个内角的平分线交于点O,过点O作 ,交边AB于点D.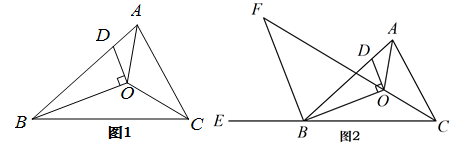
(1)、如图1,
①若∠ABC=40°,则∠AOC= , ∠ADO=;
②猜想∠AOC与∠ADO的关系,并说明你的理由。
(2)、如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F . 若∠AOC=105°,∠F=32°,则∠AOD=°.
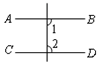
13. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.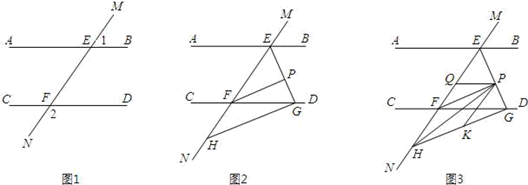 (1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
(1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.三、真题演练
-
14. 一把直尺和一块三角板 (含 、 角)如图所示摆放,直尺一边与三角板的两直角边分别交于点 和点 ,另一边与三角板的两直角边分别交于点 和点 ,且 ,那么 的大小为( )
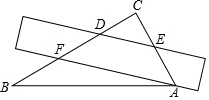 A、 B、 C、 D、15. 将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是( )
A、 B、 C、 D、15. 将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是( )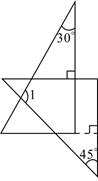 A、 B、 C、 D、16. 如图, , , ,则 的度数为( )
A、 B、 C、 D、16. 如图, , , ,则 的度数为( )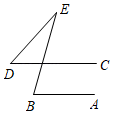 A、 B、 C、 D、17. 将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2=.
A、 B、 C、 D、17. 将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2=. 18. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
18. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )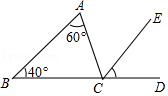 A、40° B、45° C、50° D、55°19. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是( )
A、40° B、45° C、50° D、55°19. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是( ) A、γ=2α+β B、γ=α+2β C、γ=α+β D、γ=180°﹣α﹣β
A、γ=2α+β B、γ=α+2β C、γ=α+β D、γ=180°﹣α﹣β