初中数学浙教版八年级上册1.1认识三角形（课时1） 同步训练
试卷更新日期：2019-08-08 类型：同步测试
一、三角形的定义与分类
-
1. 下面是小明用三根火柴组成的图形，其中符合三角形概念的是（ ）A、
B、
C、
D、
2. 以下由四位同学描述三角形的三种不同的说法，正确的是（ ）A、由三个角组成的图形叫三角形 B、由三条线段组成的图形叫三角形 C、由三条直线组成的图形叫三角形 D、由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形3. 图中的三角形被木板遮住了一部分，这个三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都有可能4. 若三角形的两个内角的和是85°，那么这个三角形是（ ）A、钝角三角形 B、直角三角形 C、锐角三角形 D、不能确定5. 若三角形三个内角度数比为2：3：4，则这个三角形一定是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有对
7. 如图所示，将多边形分割成三角形、图（1）中可分割出2个三角形；图（2）中可分割出3个三角形；图（3）中可分割出4个三角形；由此你能猜测出，n边形可以分割出个三角形．
8. 如图，正方形网格中每一个小正方形的边长都为1，每一个小格的顶点叫做格点．以格点为顶点分别按下列要求画三角形：
⑴在图1中，画一个三角形，使它的边长都是有理数；
⑵在图2、图3中分别画一个直角三角形，使它们的边长都是无理数，并且要求两个三角形不全等．
二、三角形三边关系
-
9. 有两根6cm、11cm的木棒，小明同学要想以这两根木棒做一个三角形，可以选用第三根木棒的长为（ ）A、3cm B、16cm C、20cm D、24cm10. 平行四边形一边的长是10cm，则这个平行四边形的两条对角线长可以是（ ）A、4cm或6cm B、6cm或8cm C、8cm或12cm D、20cm或30cm11. 已知三角形的三边长均为偶数，其中两边长分别为2和8，则第三边长为 ．12. 在△ABC中，AC=5，BC=2，且AB长为奇数．(1)、求△ABC的周长；(2)、判定△ABC的形状．13. 从1、2、3、4…、2004中任选k个数，使所选的k个数中一定可以找到能构成三角形边长的三个数（这里要求三角形三边长互不相等），试问满足条件的k的最小值是多少？14. 化简 - ，并求值。其中a与2,3分别为△ABC三边长，且a为整数。
三、内角和定理
-
15. 在△ABC中，已知 ∠A=3∠C=54° ，则∠B的度数是（ ）
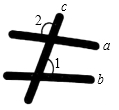
A、90° B、94° C、98° D、108°16. 如图，一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B，交斜边CD 于点A，直尺的边缘EF 分别交CD、BD 于点E、F，若∠D=60°，∠ABC=20°，则∠1 的度数为（ ）
A、25° B、40° C、50° D、80°17. 已知三角形ABC的三个内角满足关系∠B＋∠C=3∠A，则此三角形（ ）.A、一定有一个内角为45° B、一定有一个内角为60° C、一定是直角三角形 D、一定是钝角三角形18. 如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为°.
四、真题演练
-
19. 在下列长度的三条线段中，不能组成三角形的是（ ）A、2 cm， 3 cm. 4cm B、3 cm， 6 cm. 6cm C、2 cm， 2 cm， 6cm D、5 cm， 6 cm. 7 cm20. 已知三角形的两边分别为1和4，第三边长为整数 ，则该三角形的周长为（ ）A、7 B、8 C、9 D、1021. 若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（ ）A、1 B、2 C、3 D、822. 已知n正整数，若一个三角形的三边长分别是n+2、n+8、3n，则满足条件的n的值有（ ）A、4个 B、5个 C、6个 D、7个
