河北省唐山市2018-2019学年高三下学期理数第三次模拟考试试卷(B卷)
试卷更新日期:2019-08-07 类型:高考模拟
一、选择题:本题共12小题,每小题5分,共60分.
-
1. 已知集合M={x|x>3},N={xlx2-7x+10≤0},则MUN=( )A、[2,3) B、(3,5] C、(-∞,5] D、[2,+∞)2. 已知复数:满足(2+i)z=i2019 , 则:在复平面上对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 中国古代数学名著《九章算术》卷“商功”篇章中有这样的问题:“今有方锥,下方二丈七尺,高二丈九尺。问积几何?”(注:一丈等于十尺)。若此方锥的三视图如图所示(其中俯视图为正方形),则方锥的体积为( )(单位:立方尺)
 A、7047 B、21141 C、7569 D、227074. 已知 sinα+ cosα=2,则tanα=( )A、- B、 C、- D、5. 设函数y=f(x)的定义域为I.则“f(x)在I上的最大为M”是“
A、7047 B、21141 C、7569 D、227074. 已知 sinα+ cosα=2,则tanα=( )A、- B、 C、- D、5. 设函数y=f(x)的定义域为I.则“f(x)在I上的最大为M”是“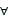 x∈I,f(x)≤M”的( ) A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 设双曲线C: (a>b>0)的两条渐近线的夹角为α.且cosα= ,则C的离心率为( )A、 B、 C、 D、27. 函数f(x)=tanx-x3的部分图象大致为( )A、
x∈I,f(x)≤M”的( ) A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 设双曲线C: (a>b>0)的两条渐近线的夹角为α.且cosα= ,则C的离心率为( )A、 B、 C、 D、27. 函数f(x)=tanx-x3的部分图象大致为( )A、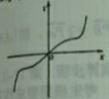 B、
B、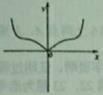 C、
C、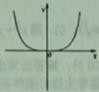 D、
D、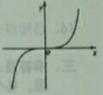 8. 一个袋子中装有大小形状完全相同的4个白球和3个黑球,从中一次摸出3个球,已知摸出球的颜色不全相同,则摸出白球个数多于黑球个数的概率为( )A、 B、 C、 D、9. 将函数f(x)=sin(ωx+ )(0>0)的图象向右平移 个单位长度,得到的图象关于y轴对称,则ω的最小值为( )A、7 B、6 C、5 D、410. 设椭圆C: (a>b>0)的左,右焦点分别为F1 , F2 , 离心率为 ,以F1F2为直径的圆与C在第一象限的交点为P,则直线PF1的斜率为( )A、 B、 C、 D、11. 在△ABC中,AB=AC, ,AD=2,△ABC的面积为2 ,则∠ADB=( )
8. 一个袋子中装有大小形状完全相同的4个白球和3个黑球,从中一次摸出3个球,已知摸出球的颜色不全相同,则摸出白球个数多于黑球个数的概率为( )A、 B、 C、 D、9. 将函数f(x)=sin(ωx+ )(0>0)的图象向右平移 个单位长度,得到的图象关于y轴对称,则ω的最小值为( )A、7 B、6 C、5 D、410. 设椭圆C: (a>b>0)的左,右焦点分别为F1 , F2 , 离心率为 ,以F1F2为直径的圆与C在第一象限的交点为P,则直线PF1的斜率为( )A、 B、 C、 D、11. 在△ABC中,AB=AC, ,AD=2,△ABC的面积为2 ,则∠ADB=( )
A、30° B、45° C、60° D、30°或60°12. 已知e是自然对数的底数,不等式x[(ex-1+1)(e 1-x+1)-(e-1+e)2]>0的解集为( )A、(-1,0)U(3,+∞) B、(-1,0)U(0,3) C、(-∞,-1)U(3,+∞) D、(-∞,-1)U(0,3)二、填空题:本题共4小题,每小题5分,共20分。
-
13. 计算定积分 =
14. 已知向量 =(m,3), =(m+2,1),若 =| |2 , 则 在 方向上的投影为。15. 在四面体ABCD中,AB=4,BC=CD=3,AC=5,且AB⊥CD,当四面体ABCD的体积最大时,其外接球的表面积为.16. 已知点P(-4 ,0),因x2+y2=16上两点A,B满足 ,则|AB|=.三、解答题:共70分
-
17. 已知数列{an}的前n项和为Sn , 且1,an , Sn成等差数列。(1)、求an , Sn;(2)、证明: .18. 如图,在直三棱柱ABC-A1B1C1中,AC=BC=4,AB=4 ,M,N分别为AB,CC1的中点。
 (1)、求证:CM∥平面B1AN;(2)、若A1M⊥B1C,求平面B1AN与平面B1MC所成锐二面角的余弦值.19. 某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若X∈[1,300],每单提成3元,若X∈(300,600],每单提成4元,若X∈(600,+∞),每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若Y=[1,400],每单提成3元,若Y∈(400,+∞),每单提成4元,小王想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
(1)、求证:CM∥平面B1AN;(2)、若A1M⊥B1C,求平面B1AN与平面B1MC所成锐二面角的余弦值.19. 某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若X∈[1,300],每单提成3元,若X∈(300,600],每单提成4元,若X∈(600,+∞),每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若Y=[1,400],每单提成3元,若Y∈(400,+∞),每单提成4元,小王想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:表1:美团外卖配送员甲送餐量统计
日送餐量x(单)
13
14
16
17
18
20
天数
2
6
12
6
2
2
表2:饿了么外卖配送员乙送餐量统计
日送餐量y(单)
11
13
14
15
16
18
天数
4
5
12
3
5
1
(1)、设美团外卖配送员月工资为f(X),饿了么外卖配送员月工资为g(Y),当X=Y∈(300,600时,比较f(X)与g(Y)的大小关系;(2)、将4月份的日送餐量的频率视为日送餐量的概率。(I)计算外卖配送员甲和乙每日送餐量的数学期望E(X)和E(Y):
(II)请利用所学的统计学知识为小王作出选择,并说明理由.
20. 已知抛物线Γ:x2=2py(p>0)的焦点为FR0,1),过F且斜率为的直线k1与l1交于才,B两点,斜率为k2(k2≠0)的直线l2与Γ相切于点P,且l2与l1不垂直,Q为AB的中点。(1)、若k1= ,求|AB|:(2)、若直线PQ 过(0,2),求21. 已知函数f(x)=xlnx- x2-ax+l,a>0,函数g(x)=f'(x).(1)、若a=ln2,求g(x)的最大值;(2)、证明:f(x)有且仅有一个零点.