四川省雅安市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. ﹣2019的倒数是( )A、﹣2019 B、2019 C、 D、2. 的结果等于( )A、9 B、﹣9 C、5 D、63. 如图是下面哪个图形的俯视图( )
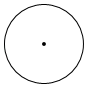 A、
A、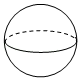 B、
B、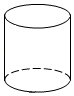 C、
C、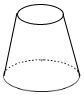 D、
D、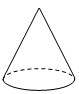 4. 不等式组 的解集为( )A、 B、 C、 D、5. 已知一组数据5,4, ,3,9的平均数为5,则这组数据的中位数是( )A、3 B、4 C、5 D、66. 下列计算中,正确的是( )A、 B、 C、 D、7. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、148. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
4. 不等式组 的解集为( )A、 B、 C、 D、5. 已知一组数据5,4, ,3,9的平均数为5,则这组数据的中位数是( )A、3 B、4 C、5 D、66. 下列计算中,正确的是( )A、 B、 C、 D、7. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、148. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、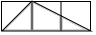 B、
B、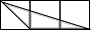 C、
C、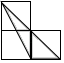 D、
D、 9. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到10. 如图,在四边形 中, , 是对角线, 分别是 的中点,连接 ,则四边形 的形状是( )
9. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到10. 如图,在四边形 中, , 是对角线, 分别是 的中点,连接 ,则四边形 的形状是( )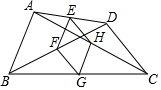 A、平行四边形 B、矩形 C、菱形 D、正方形11. 如图,已知圆 的内接六边形 的边心距 ,则该圆的内接正三角形 的面积为( )
A、平行四边形 B、矩形 C、菱形 D、正方形11. 如图,已知圆 的内接六边形 的边心距 ,则该圆的内接正三角形 的面积为( ) A、2 B、4 C、 D、12. 如图,在平面直角坐标系中,直线 与直线 交于点 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 …按此规律,则点 的纵坐标为( )
A、2 B、4 C、 D、12. 如图,在平面直角坐标系中,直线 与直线 交于点 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 …按此规律,则点 的纵坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
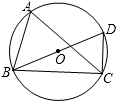
13. 在 Rt△ABC中, , ,则 .14. 化简 的结果是 .15. 如图, 内接于圆 , 是圆 的直径, ,则 的度数为 .
 16. 在两个暗盒中,各自装有编号为1,2,3的三个球,球除编号外无其它区别,则在两个暗盒中各取一个球,两球上的编号的积为偶数的概率为 .17. 已知函数 的图象如图所示,若直线 与该图象恰有三个不同的交点,则 的取值范围为 .
16. 在两个暗盒中,各自装有编号为1,2,3的三个球,球除编号外无其它区别,则在两个暗盒中各取一个球,两球上的编号的积为偶数的概率为 .17. 已知函数 的图象如图所示,若直线 与该图象恰有三个不同的交点,则 的取值范围为 .
三、解答题
-
18.(1)、计算:(2)、先化简,再求值: ,其中 .19. 某校为了解本校学生对课后服务情况的评价,随机抽取了部分学生进行调查,根据调查结果制成了如下不完整的统计图.

根据统计图:
(1)、求该校被调查的学生总数及评价为“满意”的人数;(2)、补全折线统计图;(3)、根据调查结果,若要在全校学生中随机抽1名学生,估计该学生的评价为“非常满意”或“满意”的概率是多少?20. 某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:商品
甲
乙
进价(元/件)
售价(元/件)
200
100
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)、求甲、乙两种商品的进价是多少元?(2)、若超市销售甲、乙两种商品共50件,其中销售甲种商品为 件( ),设销售完50件甲、乙两种商品的总利润为 元,求 与 之间的函数关系式,并求出 的最小值.21. 如图,平行四边形 的对角线 相交于点 ,EF经过 ,分别交 于点 , 的延长线交 的延长线于 . (1)、求证: ;(2)、若 , , ,求 的长.22. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 两点,已知
(1)、求证: ;(2)、若 , , ,求 的长.22. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 两点,已知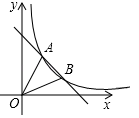 (1)、求一次函数和反比例函数的解析式;(2)、求 点的坐标;(3)、连接 ,求 的面积.
(1)、求一次函数和反比例函数的解析式;(2)、求 点的坐标;(3)、连接 ,求 的面积.

