四川省内江市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. ﹣268000用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体中,主视图为三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列事件为必然事件的是( )A、袋中有4个蓝球,2个绿球,共6个球,随机摸出一个球是红球 B、三角形的内角和为180° C、打开电视机,任选一个频道,屏幕上正在播放广告 D、抛掷一枚硬币两次,第一次正面向上,第二次反面向上5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
4. 下列事件为必然事件的是( )A、袋中有4个蓝球,2个绿球,共6个球,随机摸出一个球是红球 B、三角形的内角和为180° C、打开电视机,任选一个频道,屏幕上正在播放广告 D、抛掷一枚硬币两次,第一次正面向上,第二次反面向上5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 在函数 中,自变量x的取值范围是( )A、 B、 且 C、 D、 且8. 如图,在 中, , , , ,则 的长为( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 在函数 中,自变量x的取值范围是( )A、 B、 且 C、 D、 且8. 如图,在 中, , , , ,则 的长为( )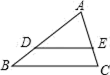 A、6 B、7 C、8 D、99. 一个等腰三角形的底边长是6,腰长是一元二次方程 的一根,则此三角形的周长是( )A、16 B、12 C、14 D、12或1610. 如图,在 中, , , ,将 绕点 顺时针旋转度得到 ,当点 的对应点 恰好落在 边上时,则 的长为( )
A、6 B、7 C、8 D、99. 一个等腰三角形的底边长是6,腰长是一元二次方程 的一根,则此三角形的周长是( )A、16 B、12 C、14 D、12或1610. 如图,在 中, , , ,将 绕点 顺时针旋转度得到 ,当点 的对应点 恰好落在 边上时,则 的长为( )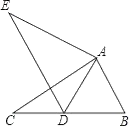 A、1.6 B、1.8 C、2 D、2.611. 若关于 的代等式组 恰有三个整数解,则 的取值范围是( )A、 B、 C、 D、 或12. 如图,将 沿着过 的中点 的直线折叠,使点 落在 边上的 处,称为第一次操作,折痕 到 的距离为 ;还原纸片后,再将 沿着过 的中点 的直线折叠,使点 落在 边上的 处,称为第二次操作,折痕 到 的距离记为 ;按上述方法不断操作下去……经过第 次操作后得到折痕 ,到 的距离记为 .若 ,则 的值为( )
A、1.6 B、1.8 C、2 D、2.611. 若关于 的代等式组 恰有三个整数解,则 的取值范围是( )A、 B、 C、 D、 或12. 如图,将 沿着过 的中点 的直线折叠,使点 落在 边上的 处,称为第一次操作,折痕 到 的距离为 ;还原纸片后,再将 沿着过 的中点 的直线折叠,使点 落在 边上的 处,称为第二次操作,折痕 到 的距离记为 ;按上述方法不断操作下去……经过第 次操作后得到折痕 ,到 的距离记为 .若 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
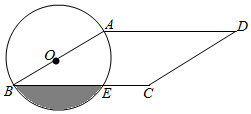
13. 分解因式:xy2﹣2xy+x= .14. 一组数据为0,1,2,3,4,则这组数据的方差是 .15. 若 ,则分式 的值为 .16. 如图,在平行四边形ABCD中,AB<AD,∠C=150°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为 .
 17. 若 ,则 .18. 如图,点 在同一直线上,且 ,点 分别是 的中点,分别以 为边,在 同侧作三个正方形,得到三个平行四边形(阴影部分)的面积分别记作 ,若 ,则 .
17. 若 ,则 .18. 如图,点 在同一直线上,且 ,点 分别是 的中点,分别以 为边,在 同侧作三个正方形,得到三个平行四边形(阴影部分)的面积分别记作 ,若 ,则 . 19. 若 为实数,且 ,则代数式 的最大值是 .20. 如图,在菱形 中, ,点 分别在边 上,将四边形 沿 翻折,使 的对应线段 经过顶点 ,当 时, 的值是 .
19. 若 为实数,且 ,则代数式 的最大值是 .20. 如图,在菱形 中, ,点 分别在边 上,将四边形 沿 翻折,使 的对应线段 经过顶点 ,当 时, 的值是 .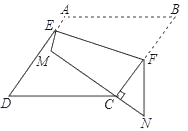
三、解答题
-
21. 计算: .22. 如图,在正方形 中,点 是 上的一点,点 是 延长线上的一点,且 ,连结 .
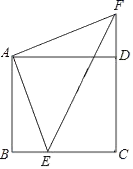 (1)、求证: ≌ ;(2)、若 ,请求出 的长.23. “大千故里,文化内江”,我市某中学为传承大千艺术精神,征集学生书画作品.王老师从全校20个班中随机抽取了 4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
(1)、求证: ≌ ;(2)、若 ,请求出 的长.23. “大千故里,文化内江”,我市某中学为传承大千艺术精神,征集学生书画作品.王老师从全校20个班中随机抽取了 4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图. (1)、王老师采取的调查方式是(填“普查”或“抽样调査”),王老师所调查的4个班共征集到作品件,并补全条形统计图;(2)、在扇形统计图中,表示 班的扇形周心角的度数为;(3)、如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)24. 如图,两座建筑物 与 ,其中 的高为120米,从 的顶点 测得 顶部 的仰角为30°,测得其底部 的俯角为45°,求这两座建筑物的地面距离 为多少米?(结果保留根号)
(1)、王老师采取的调查方式是(填“普查”或“抽样调査”),王老师所调查的4个班共征集到作品件,并补全条形统计图;(2)、在扇形统计图中,表示 班的扇形周心角的度数为;(3)、如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)24. 如图,两座建筑物 与 ,其中 的高为120米,从 的顶点 测得 顶部 的仰角为30°,测得其底部 的俯角为45°,求这两座建筑物的地面距离 为多少米?(结果保留根号)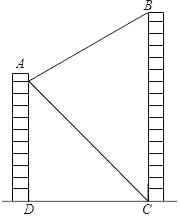 25. 如图,一次函数 的图象与反比例函数 的图象交于第二、四象限内的点 和点 .过点 作 轴的垂线,垂足为点 , 的面积为4.
25. 如图,一次函数 的图象与反比例函数 的图象交于第二、四象限内的点 和点 .过点 作 轴的垂线,垂足为点 , 的面积为4. (1)、分别求出 和 的值;(2)、结合图象直接写出 的解集;(3)、在 轴上取点 ,使 取得最大值时,求出点 的坐标.26. 某商店准备购进 两种商品, 种商品毎件的进价比 种商品每件的进价多20元,用3000元购进 种商品和用1800元购进 种商品的数量相同.商店将 种商品每件的售价定为80元, 种商品每件的售价定为45元.(1)、 种商品每件的进价和 种商品每件的进价各是多少元?(2)、商店计划用不超过1560元的资金购进 两种商品共40件,其中 种商品的数量不低于 种商品数量的一半,该商店有几种进货方案?(3)、端午节期间,商店开展优惠促销活动,决定对每件 种商品售价优惠 ( )元, 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.27. 与⊙ 相切于点 ,直线 与⊙ 相离, 于点 ,且 , 与⊙ 交于点 , 的延长线交直线 于点 .
(1)、分别求出 和 的值;(2)、结合图象直接写出 的解集;(3)、在 轴上取点 ,使 取得最大值时,求出点 的坐标.26. 某商店准备购进 两种商品, 种商品毎件的进价比 种商品每件的进价多20元,用3000元购进 种商品和用1800元购进 种商品的数量相同.商店将 种商品每件的售价定为80元, 种商品每件的售价定为45元.(1)、 种商品每件的进价和 种商品每件的进价各是多少元?(2)、商店计划用不超过1560元的资金购进 两种商品共40件,其中 种商品的数量不低于 种商品数量的一半,该商店有几种进货方案?(3)、端午节期间,商店开展优惠促销活动,决定对每件 种商品售价优惠 ( )元, 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.27. 与⊙ 相切于点 ,直线 与⊙ 相离, 于点 ,且 , 与⊙ 交于点 , 的延长线交直线 于点 . (1)、求证: ;(2)、若⊙ 的半径为3,求线段 的长;(3)、若在⊙ 上存在点 ,使 是以 为底边的等腰三角形,求⊙ 的半径 的取值范围.28. 两条抛物线 与 的顶点相同.
(1)、求证: ;(2)、若⊙ 的半径为3,求线段 的长;(3)、若在⊙ 上存在点 ,使 是以 为底边的等腰三角形,求⊙ 的半径 的取值范围.28. 两条抛物线 与 的顶点相同. (1)、求抛物线 的解析式;(2)、点 是抛物找 在第四象限内图象上的一动点,过点 作 轴, 为垂足,求 的最大值;(3)、设抛物线 的顶点为点 ,点 的坐标为 ,问在 的对称轴上是否存在点 ,使线段 绕点 顺时针旋转90°得到线段 ,且点 恰好落在抛物线 上?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线 的解析式;(2)、点 是抛物找 在第四象限内图象上的一动点,过点 作 轴, 为垂足,求 的最大值;(3)、设抛物线 的顶点为点 ,点 的坐标为 ,问在 的对称轴上是否存在点 ,使线段 绕点 顺时针旋转90°得到线段 ,且点 恰好落在抛物线 上?若存在,求出点 的坐标;若不存在,请说明理由.