四川省泸州市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. -8的绝对值是( )A、8 B、-8 C、 D、-2. 将 用科学记数法表示为( )A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 下列立体图形中,俯视图是三角形的是( )A、
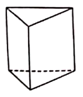 B、
B、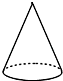 C、
C、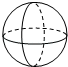 D、
D、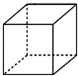 5. 函数 的自变量 的取值范围是( )A、 B、 C、 D、6. 如图, ,垂足为点 , , ,则 的度数为( )
5. 函数 的自变量 的取值范围是( )A、 B、 C、 D、6. 如图, ,垂足为点 , , ,则 的度数为( )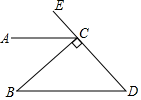 A、 B、 C、 D、7. 把 分解因式,结果正确的是( )A、 B、 C、 D、8. 四边形 的对角线 与 相交于点 ,下列四组条件中,一定能判定四边形 为平行四边形的是( )A、 B、 , C、 , D、9. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )
A、 B、 C、 D、7. 把 分解因式,结果正确的是( )A、 B、 C、 D、8. 四边形 的对角线 与 相交于点 ,下列四组条件中,一定能判定四边形 为平行四边形的是( )A、 B、 , C、 , D、9. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )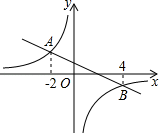 A、 或 B、 或 C、 或 D、 或10. 一个菱形的边长为 ,面积为 ,则该菱形的两条对角线的长度之和为( )A、 B、 C、 D、11. 如图,等腰 的内切圆⊙ 与 , , 分别相切于点 , , ,且 , ,则 的长是( )
A、 或 B、 或 C、 或 D、 或10. 一个菱形的边长为 ,面积为 ,则该菱形的两条对角线的长度之和为( )A、 B、 C、 D、11. 如图,等腰 的内切圆⊙ 与 , , 分别相切于点 , , ,且 , ,则 的长是( )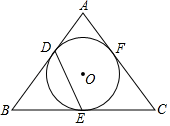 A、 B、 C、 D、12. 已知二次函数 (其中 是自变量)的图象与 轴没有公共点,且当 时, 随 的增大而减小,则实数 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知二次函数 (其中 是自变量)的图象与 轴没有公共点,且当 时, 随 的增大而减小,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
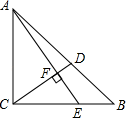
13. 4的算术平方根是 , 9的平方根是 , ﹣27的立方根是 .14. 在平面直角坐标系中,点 与点 关于 轴对称,则 的值是 .15. 已知 , 是一元二次方程 的两实根,则 的值是 .16. 如图,在等腰 中, , ,点 在边 上, ,点 在边 上, ,垂足为 ,则 长为 .
三、解答题
-
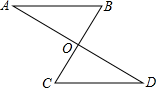
17. 计算: .18. 如图, , 和 相交于点 , .求证: .
 19. 化简: .20. 某市气象局统计了5月1日至8日中午12时的气温(单位 ),整理后分别绘制成如图所示的两幅统计图.
19. 化简: .20. 某市气象局统计了5月1日至8日中午12时的气温(单位 ),整理后分别绘制成如图所示的两幅统计图.根据图中给出的信息,解答下列问题:
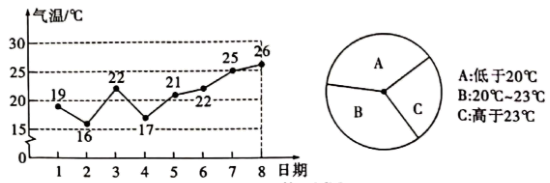 (1)、该市5月1日至8日中午时气温的平均数是 ,中位数是 ;(2)、求扇形统计图中扇形 的圆心角的度数;(3)、现从该市5月1日至5日的 天中,随机抽取 天,求恰好抽到 天中午12时的气温均低于 的概率.21. 某出租汽车公司计划购买 型和 型两种节能汽车,若购买 型汽车 辆, 型汽车 辆,共需 万元;若购买 型汽车 辆, 型汽车 辆,共需 万元.(1)、 型和 型汽车每辆的价格分别是多少万元?(2)、该公司计划购买 型和 型两种汽车共 辆,费用不超过 万元,且 型汽车的数量少于 型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.22. 一次函数 的图象经过点 , .(1)、求该一次函数的解析式;(2)、若该一次函数的图象与反比例函数 的图象相交于 , 两点,且 ,求 的值.23. 如图,海中有两个小岛 , ,某渔船在海中的 处测得小岛D位于东北方向上,且相距 ,该渔船自西向东航行一段时间到达点 处,此时测得小岛 恰好在点 的正北方向上,且相距 ,又测得点 与小岛 相距 .
(1)、该市5月1日至8日中午时气温的平均数是 ,中位数是 ;(2)、求扇形统计图中扇形 的圆心角的度数;(3)、现从该市5月1日至5日的 天中,随机抽取 天,求恰好抽到 天中午12时的气温均低于 的概率.21. 某出租汽车公司计划购买 型和 型两种节能汽车,若购买 型汽车 辆, 型汽车 辆,共需 万元;若购买 型汽车 辆, 型汽车 辆,共需 万元.(1)、 型和 型汽车每辆的价格分别是多少万元?(2)、该公司计划购买 型和 型两种汽车共 辆,费用不超过 万元,且 型汽车的数量少于 型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.22. 一次函数 的图象经过点 , .(1)、求该一次函数的解析式;(2)、若该一次函数的图象与反比例函数 的图象相交于 , 两点,且 ,求 的值.23. 如图,海中有两个小岛 , ,某渔船在海中的 处测得小岛D位于东北方向上,且相距 ,该渔船自西向东航行一段时间到达点 处,此时测得小岛 恰好在点 的正北方向上,且相距 ,又测得点 与小岛 相距 .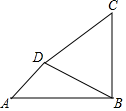 (1)、求 的值;(2)、求小岛 , 之间的距离(计算过程中的数据不取近似值).24. 如图, 为⊙ 的直径,点 在 的延长线上,点 在⊙ 上,且 .
(1)、求 的值;(2)、求小岛 , 之间的距离(计算过程中的数据不取近似值).24. 如图, 为⊙ 的直径,点 在 的延长线上,点 在⊙ 上,且 . (1)、求证: 是⊙ 的切线;(2)、已知 , ,点 是 的中点, ,垂足为 , 交 于点 ,求 的长.25. 如图,在平面直角坐标系xOy中,已知二次函数y=ax+bx+c的图像经过点A(-2,0),C(0,-6)。其对称轴为直线x=2
(1)、求证: 是⊙ 的切线;(2)、已知 , ,点 是 的中点, ,垂足为 , 交 于点 ,求 的长.25. 如图,在平面直角坐标系xOy中,已知二次函数y=ax+bx+c的图像经过点A(-2,0),C(0,-6)。其对称轴为直线x=2 (1)、求该二次函数的解析式;(2)、若直线 将△AOC的面积分成相等的两部分,求m的值;(3)、点B是该二次函数图象与x轴的另一交点,点D是直线x=2上位于x轴下方的动点,点E是第四象限内该二次函数图象上的动点,且位于直线x=2右侧。若以点E为直角顶点的△BED与△AOC相似,求点E的坐标。
(1)、求该二次函数的解析式;(2)、若直线 将△AOC的面积分成相等的两部分,求m的值;(3)、点B是该二次函数图象与x轴的另一交点,点D是直线x=2上位于x轴下方的动点,点E是第四象限内该二次函数图象上的动点,且位于直线x=2右侧。若以点E为直角顶点的△BED与△AOC相似,求点E的坐标。