四川省巴中市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
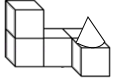
1. 下列四个算式中,正确的是( )A、 B、 C、 D、2. 在平面直角坐标系中,已知点A(﹣4,3)与点B关于原点对称,则点B的坐标为( )A、(﹣4,﹣3) B、(4,3) C、(4,﹣3) D、(﹣4,3)3. 企业家陈某,在家乡投资9300万元,建立产业园区2万余亩.将9300万元用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元4. 如图是由一些小立方体与圆锥组合成的立体图形,它的主视图是( )
 A、
A、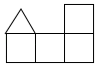 B、
B、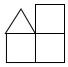 C、
C、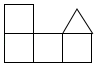 D、
D、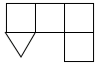 5. 已知关于x、y的二元一次方程组 的解是 ,则 的值是( )A、1 B、2 C、﹣1 D、06. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是矩形 C、对角线互相垂直的矩形是正方形 D、四边相等的平行四边形是正方形7. 如图所示,是巴中某校对学生到校方式的情况统计图.若该校骑自行车到校的学生有200人,则步行到校的学生有( )
5. 已知关于x、y的二元一次方程组 的解是 ,则 的值是( )A、1 B、2 C、﹣1 D、06. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是矩形 C、对角线互相垂直的矩形是正方形 D、四边相等的平行四边形是正方形7. 如图所示,是巴中某校对学生到校方式的情况统计图.若该校骑自行车到校的学生有200人,则步行到校的学生有( ) A、120人 B、160人 C、125人 D、180人8. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
A、120人 B、160人 C、125人 D、180人8. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )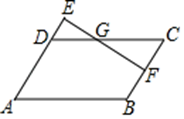 A、2:3 B、3:2 C、9:4 D、4:99. 如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A、2:3 B、3:2 C、9:4 D、4:99. 如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )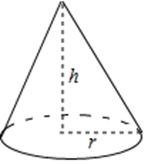 A、15π B、30π C、45π D、60π10. 二次函数 的图象如图所示,下列结论① ,② ,③ ,④ .其中正确的是( )
A、15π B、30π C、45π D、60π10. 二次函数 的图象如图所示,下列结论① ,② ,③ ,④ .其中正确的是( )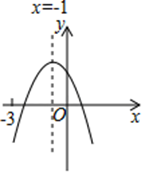 A、①④ B、②④ C、②③ D、①②③④
A、①④ B、②④ C、②③ D、①②③④二、填空题
-
11. 函数 自变量x的取值范围是 .12. 如果一组数据为4、a、5、3、8,其平均数为a,那么这组数据的方差为 .13. 如图,反比例函数 经过A、B两点,过点A作 轴于点C,过点B作 轴于点D,过点B作 轴于点E,连结AD,已知 、 、 .则 = .
 14. 若关于x的分式方程 有增根,则m的值为 .15. 如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若 , , .则 = .
14. 若关于x的分式方程 有增根,则m的值为 .15. 如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若 , , .则 = .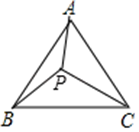
三、解答题
-
16. 计算 .17. 已知实数x、y满足 ,求代数式 的值.18. 如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
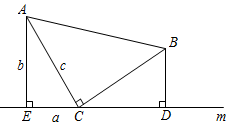
①求证: ;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
19. △ABC在边长为l的正方形网格中如图所示.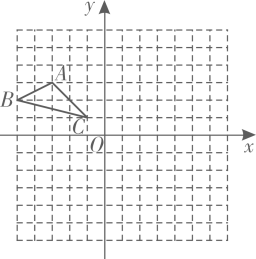
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
20. 在“扶贫攻坚”活动中,某单位计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.①请问甲、乙两种物品的单价各为多少?
②如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5050元,通过计算得出共有几种选购方案?
21. 如图表示的是某班部分同学衣服上口袋的数目.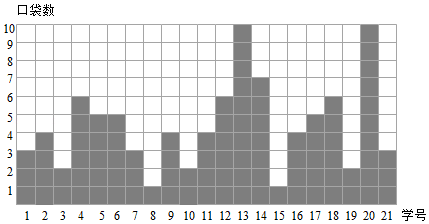
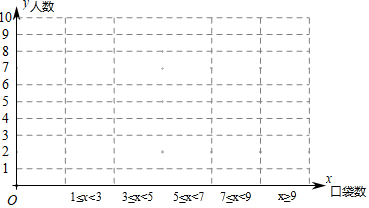 (1)、从图中给出的信息得到学生衣服上口袋数目的中位数为 , 众数为 .(2)、根据如图信息,在给出的图表中绘制频数条形统计图,由此估计该班学生衣服上口袋数目为 的概率.22. 已知关于x的一元二次方程 有两不相等的实数根.
(1)、从图中给出的信息得到学生衣服上口袋数目的中位数为 , 众数为 .(2)、根据如图信息,在给出的图表中绘制频数条形统计图,由此估计该班学生衣服上口袋数目为 的概率.22. 已知关于x的一元二次方程 有两不相等的实数根.①求m的取值范围.
②设x1 , x2是方程的两根且 ,求m的值.
23. 某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得 , ,求出点D到AB的距离.(参考数据 , , )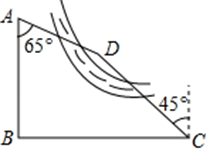 24. 如图,一次函数 (k1、b为常数,k1≠0)的图象与反比例函数 的图象交于点A(m,8)与点B(4,2).
24. 如图,一次函数 (k1、b为常数,k1≠0)的图象与反比例函数 的图象交于点A(m,8)与点B(4,2).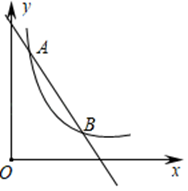
①求一次函数与反比例函数的解析式.
②根据图象说明,当x为何值时, .
25. 如图,在菱形ABCD中,连结BD、AC交于点O,过点O作 于点H,以点O为圆心,OH为半径的半圆交AC于点M.
①求证:DC是⊙O的切线.
②若 且 ,求图中阴影部分的面积.
③在②的条件下,P是线段BD上的一动点,当PD为何值时, 的值最小,并求出最小值.
26. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.