山东省枣庄市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 下列运算,正确的是( )A、 B、 C、 D、x6÷x3=x22. 下列图形,可以看作中心对称图形的是( )A、
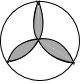 B、
B、 C、
C、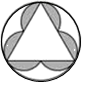 D、
D、 3. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。
3. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。 A、45° B、60° C、75° D、85°4. 如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过点 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是( )
A、45° B、60° C、75° D、85°4. 如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过点 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是( )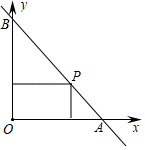 A、 B、 C、 D、5. 从﹣1、2、3、﹣6这四个数中任取两数,分别记为 、 ,那么点 在函数 图象的概率是( )A、 B、 C、 D、6. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )
A、 B、 C、 D、5. 从﹣1、2、3、﹣6这四个数中任取两数,分别记为 、 ,那么点 在函数 图象的概率是( )A、 B、 C、 D、6. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )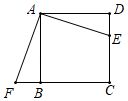 A、4 B、 C、6 D、7. 如图,在边长为4的正方形 中,以点 为圆心, 为半径画弧,交对角线 于点 ,则图中阴影部分的面积是(结果保留 )( )
A、4 B、 C、6 D、7. 如图,在边长为4的正方形 中,以点 为圆心, 为半径画弧,交对角线 于点 ,则图中阴影部分的面积是(结果保留 )( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,等腰直角三角形 的顶点 、 分别在 轴、 轴的正半轴上, , 轴,点 在函数 的图象上,若 ,则 的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,等腰直角三角形 的顶点 、 分别在 轴、 轴的正半轴上, , 轴,点 在函数 的图象上,若 ,则 的值为( )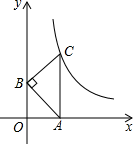 A、1 B、 C、 D、29. 如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是( )
A、1 B、 C、 D、29. 如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 点 在数轴上的位置如图所示, 为原点, , .若点 所表示的数为 ,则点 所表示的数为( )
10. 点 在数轴上的位置如图所示, 为原点, , .若点 所表示的数为 ,则点 所表示的数为( )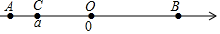 A、 B、 C、 D、11. 如图,将 沿 边上的中线 平移到 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于( )
A、 B、 C、 D、11. 如图,将 沿 边上的中线 平移到 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于( ) A、2 B、3 C、4 D、
A、2 B、3 C、4 D、二、填空题
-
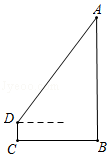
12. 若 ,则 .13. 已知关于 的方程 有两个不相等的实数根,则 的取值范围是 .14. 如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
 15. 用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形 .图中, 度.
15. 用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形 .图中, 度.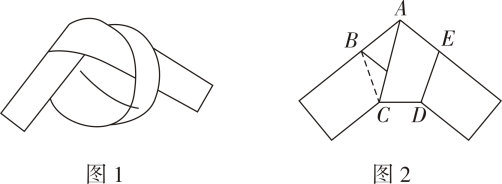 16. 把两个同样大小含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 ,且另外三个锐角顶点 在同一直线上.若 ,则 .
16. 把两个同样大小含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 ,且另外三个锐角顶点 在同一直线上.若 ,则 .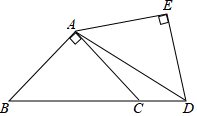 17. 观察下列各式:
17. 观察下列各式:,
,
,
请利用你发现的规律,计算:
,其结果为 .
三、解答题
-
18. 先化简,再求值: ,其中 为整数且满足不等式组19. 如图, 是菱形 的对角线, ,
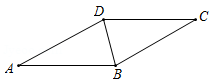 (1)、请用尺规作图法,作 的垂直平分线 ,垂足为 ,交 于 ;(不要求写作法,保留作图痕迹)(2)、在(1)条件下,连接 ,求 的度数.20. 对于任意实数 、 ,定义关于“ ”的一种运算如下: .例如 .(1)、求 的值;(2)、若 ,且 ,求 的值.21. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
(1)、请用尺规作图法,作 的垂直平分线 ,垂足为 ,交 于 ;(不要求写作法,保留作图痕迹)(2)、在(1)条件下,连接 ,求 的度数.20. 对于任意实数 、 ,定义关于“ ”的一种运算如下: .例如 .(1)、求 的值;(2)、若 ,且 ,求 的值.21. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:(一)、数据收集,从全校随机抽取20学生,进行每周用于课外阅读时间的调查,数据如下(单位: ):
30
60
81
50
44
110
130
146
80
100
60
80
120
140
75
81
10
30
81
92
(二)、整理数据,按如下分段整理样本数据并补全表格:
课外阅读时间
等级
人数
3
8
(三)、分析数据,补全下列表格中的统计量:
平均数
中位数
众数
80
81
(四)、得出结论:
①表格中的数据: , , ;
②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为;
③如果该校现有学生400人,估计等级为“ ”的学生有人;
④假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读本课外书.
22. 如图,在 中, ,以 为直径作 ,点 为 上一点,且 ,连接 并延长交 的延长线于点 .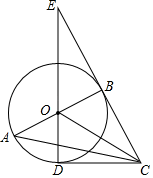 (1)、判断直线 与 的位置关系,并说明理由;(2)、若 , ,求圆的半径及 的长.23. 在 中, , , 于点 .
(1)、判断直线 与 的位置关系,并说明理由;(2)、若 , ,求圆的半径及 的长.23. 在 中, , , 于点 .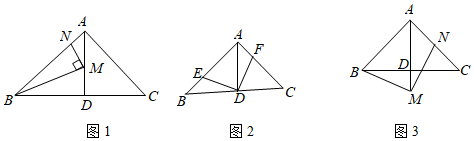 (1)、如图1,点 , 分别在 , 上,且 ,当 , 时,求线段 的长;(2)、如图2,点 , 分别在 , 上,且 ,求证: ;(3)、如图3,点 在 的延长线上,点 在 上,且 ,求证: .24. 已知抛物线 的对称轴是直线 ,与 轴相交于 , 两点(点 在点 右侧),与 轴交于点 .
(1)、如图1,点 , 分别在 , 上,且 ,当 , 时,求线段 的长;(2)、如图2,点 , 分别在 , 上,且 ,求证: ;(3)、如图3,点 在 的延长线上,点 在 上,且 ,求证: .24. 已知抛物线 的对称轴是直线 ,与 轴相交于 , 两点(点 在点 右侧),与 轴交于点 .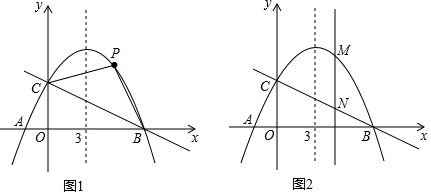 (1)、求抛物线的解析式和 , 两点的坐标;(2)、如图1,若点 是抛物线上 、 两点之间的一个动点(不与 、 重合),是否存在点 ,使四边形 的面积最大?若存在,求点 的坐标及四边形 PBOC 面积的最大值;若不存在,请说明理由;
(1)、求抛物线的解析式和 , 两点的坐标;(2)、如图1,若点 是抛物线上 、 两点之间的一个动点(不与 、 重合),是否存在点 ,使四边形 的面积最大?若存在,求点 的坐标及四边形 PBOC 面积的最大值;若不存在,请说明理由;
(3)、如图2,若点 是抛物线上任意一点,过点 作 轴的平行线,交直线 于点 ,当 时,求点 的坐标.