山东省东营市2019年中考数学试卷

试卷更新日期：2019-08-06 类型：中考真卷

进入出卷网下载

一、单选题

1. $- 2019$ 的相反数是（）

A、 $- 2019$ B、 $2019$ C、 $- \frac{1}{2019}$ D、 $\frac{1}{2019}$

查看试题解析
2. 下列运算正确的是（）

A、 $3 x^{3} ﹣ 5 x^{3} ＝ - 2 x$ B、 $8 x^{3} \div 4 x ＝ 2 x$ C、 $\frac{x y}{x y - y^{2}} = \frac{x}{x - y}$ D、 $\sqrt{3} + \sqrt{7} = \sqrt{10}$

查看试题解析
3. 将一副三角板（ $∠ A ＝ 30 ° ， ∠ E ＝ 45 °$ ）按如图所示方式摆放，使得 $B A / / E F$ ，则 $∠ A O F$ 等于（）

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $115 °$

查看试题解析
4. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 篮球联赛中，每场比赛都要分出胜负，每队胜 $1$ 场得 $2$ 分，负 $1$ 场得 $1$ 分，某队在 $10$ 场比赛中得到 $16$ 分．若设该队胜的场数为 $x$ ，负的场数为 $y$ ，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 10 \\ 2 x + y = 16 \end{array}$ B、 ${\begin{array}{l} x + y = 10 \\ 2 x - y = 16 \end{array}$ C、 ${\begin{array}{l} x + y = 10 \\ x - 2 y = 16 \end{array}$ D、 ${\begin{array}{l} x + y = 10 \\ x + 2 y = 16 \end{array}$

查看试题解析
6. 从1，2，3，4中任取两个不同的数，分别记为 $a$ 和 $b$ ，则 $a^{2} + b^{2} > 19$ 的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{5}{12}$ C、 $\frac{7}{12}$ D、 $\frac{1}{3}$

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ A C B ＝ 90 °$ ，分别以点 $B$ 和点 $C$ 为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于 $D ， E$ 两点，作直线 $D E$ 交 $A B$ 于点 $F$ ，交 $B C$ 于点 $G$ ，连结 $C F$ ．若 $A C ＝ 3 ， C G ＝ 2$ ，则 $C F$ 的长为（）

A、 $\frac{5}{2}$ B、 $3$ C、 $2$ D、 $\frac{7}{2}$

查看试题解析
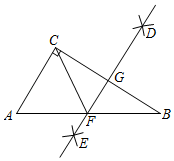8. 甲、乙两队参加了“端午情，龙舟韵”赛龙舟比赛，两队在比赛时的路程 $s$ （米）与时间 $t$ （秒）之间的函数图象如图所示，请你根据图象判断，下列说法正确的是（）

A、乙队率先到达终点 B、甲队比乙队多走了 $126$ 米 C、在 $47.8$ 秒时，两队所走路程相等 D、从出发到 $13.7$ 秒的时间段内，乙队的速度慢

查看试题解析
9. 如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点 $B$ 出发，沿表面爬到 $A C$ 的中点 $D$ 处，则最短路线长为（）

A、 $3 \sqrt{2}$ B、 $\frac{3 \sqrt{3}}{2}$ C、 $3$ D、 $3 \sqrt{3}$

查看试题解析
10. 如图，在正方形 $A B C D$ 中，点 $O$ 是对角线 $A C ， B D$ 的交点，过点 $O$ 作射线分别交 $O M ， O N$ 于点 $E ， F$ ，且 $∠ E O F ＝ 90 °$ ，交 $O C ， E F$ 于点 $G$ ．给出下列结论： $① △ C O E ≌ △ D O F$ ； $② △ O G E ∽ △ F G C$ C； $③$ 四边形 $C E O F$ 的面积为正方形 $A B C D$ 面积的 $\frac{1}{4}$ ； $④ D F^{2} + B E^{2} ＝ O G • O C$ ．其中正确的是（）

A、 $① ② ③ ④$ B、 $① ② ③$ C、 $① ② ④$ D、 $③ ④$

查看试题解析

二、填空题

11. 2019年1月12日，“五指山”舰正式入列服役，是我国第六艘型综合登陆舰艇，满载排水量超过20000吨，20000用科学记数法表示为．

查看试题解析
12. 因式分解： $x (x - 3) - x + 3 =$ ．

查看试题解析
13. 东营市某中学为积极响应“书香东营，全民阅读”活动，助力学生良好阅读习惯的养成，形成浓厚的阅读氛围，随机调查了部分学生平均每天的阅读时间，统计结果如表所示，则在本次调查中，学生阅读时间的中位数是．

时间（小时）

0.5

1

1.5

2

2.5

人数（人）

12

22

10

5

3

查看试题解析
14. 已知等腰三角形的底角是 $30 °$ ，腰长为 $2 \sqrt{3}$ ，则它的周长是．

查看试题解析
15. 不等式组 ${\begin{array}{l} x - 3 (x - 2) > 4 \\ \frac{2 x - 1}{5} \leq \frac{x + 1}{2} \end{array}$ 的解集为．

查看试题解析
16. 如图， $A C$ 是 $⊙ O$ 的弦， $A C ＝ 5$ ，点 $B$ 是 $⊙ O$ 上的一个动点，且 $∠ A B C ＝ 45 °$ ，若点 $M ， N$ 分别是 $A C ， B C$ 的中点，则 $M N$ 的最大值是．

查看试题解析
17. 如图，在平面直角坐标系中， $△ A C E$ 是以菱形 $A B C D$ 的对角线 $A C$ 为边的等边三角形， $A C ＝ 2 ，$ 点 $C$ 与点 $E$ 关于 $x$ 轴对称，则点 $D$ 的坐标是．

查看试题解析
18. 如图，在平面直角坐标系中，函数 $y = \frac{\sqrt{3}}{3} x$ 和 $y = - \sqrt{3} x$ 的图象分别为直线 $l_{1} ， l_{2}$ ，过 $l_{1}$ 上的点 $A_{1} (1 ， \frac{\sqrt{3}}{3})$ 作 $x$ 轴的垂线交 $l_{2}$ 于点 $A_{2}$ ，过点 $A_{2}$ 作 $y$ 轴的垂线交 $l_{1}$ 于点 $A_{3}$ ，过点 $A_{3}$ 作 $x$ 轴的垂线交 $l_{2}$ 于点 $A_{4}$ ，…依次进行下去，则点 $A_{2019}$ 的横坐标为．

查看试题解析

三、解答题

19.

(1)、计算： ${(\frac{1}{2019})}^{- 1} + {(3.14 - π)}^{0}$ $+ | 2 \sqrt{3} - \sqrt{2} | + 2 \sin 45^{\circ} - \sqrt{12}$ ；

(2)、化简求值： $(\frac{a}{a - b} - \frac{b^{2}}{a^{2} - a b}) \div \frac{a^{2} + 2 a b + b^{2}}{a}$ ，当 $a = - 1$ 时，请你选择一个适当的数作为 $b$ 的值，代入求值．

查看试题解析
20. 为庆祝建国 $70$ 周年，东营市某中学决定举办校园艺术节．学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加．为了了解报名情况，组委会在全校随机抽取了若干名学生进行问卷调查，现将报名情况绘制成如图所示的不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

(1)、在这次调查中，一共抽取了多少名学生？

(2)、补全条形统计图；

(3)、在扇形统计图中，求“声乐”类对应扇形圆心角的度数；

(4)、小东和小颖报名参加“器乐”类比赛，现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器，用列表法或画树状图法求出他们选中同一种乐器的概率．

查看试题解析
21. 如图， $A B$ 是 $⊙ O$ 的直径，点 $D$ 是 $A B$ 延长线上的一点，点 $C$ 在 $⊙ O$ 上，且AC=CD， $∠ A C D ＝ 120 °$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径为 $3$ ，求图中阴影部分的面积．

查看试题解析
22. 如图，在平面直角坐标系中，直线 $y = m x$ 与双曲线 $y = \frac{n}{x}$ 相交于 $A (- 2 ， a) ， B$ 两点， $B C ⊥ x$ 轴，垂足为 $C$ ， $△ A O C$ 的面积是 $2$ ．

(1)、求 $m ， n$ 的值；

(2)、求直线 $A C$ 的解析式．

查看试题解析
23. 为加快新旧动能转换，提高公司经济效益，某公司决定对近期研发出的一种电子产品进行降价促销，使生产的电子产品能够及时售出，根据市场调查：这种电子产品销售单价定为 $200$ 元时，每天可售出 $300$ 个；若销售单价每降低 $1$ 元，每天可多售出 $5$ 个．已知每个电子产品的固定成本为 $100$ 元，问这种电子产品降价后的销售单价为多少元时，公司每天可获利 $32000$ 元？

查看试题解析
24. 如图1，在 $R t △ A B C$ 中， $∠ B ＝ 90 ° ， A B ＝ 4 ， B C ＝ 2$ ，点 $D ， E$ 分别是边 $B C ， A C$ 的中点，连接 $D E$ ．将 $△ C D E$ 绕点 $C$ 逆时针方向旋转，记旋转角为 $α$ ．

(1)、问题发现
$①$ 当 $α = 0^{\circ}$ 时， $\frac{A E}{B D} =$ ； $②$ 当 $α = 180^{\circ}$ 时， $\frac{A E}{B D} =$ ．

(2)、拓展探究
试判断：当 $0 ° \leq α < 360 °$ 时， $\frac{A E}{B D}$ 的大小有无变化？请仅就图2的情形给出证明．

(3)、问题解决
$△ C D E$ 绕点 $C$ 逆时针旋转至 $A ， B ， E$ 三点在同一条直线上时，求线段 $B D$ 的长．

查看试题解析
25. 已知抛物线 $y ＝ a x^{2} + b x ﹣ 4$ 经过点 $A (2 ， 0) ， B (- 4 ， 0)$ ，与 $y$ 轴交于点 $C$ ．

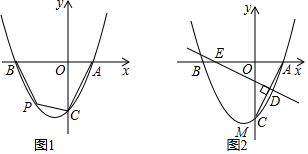(1)、求这条抛物线的解析式；

(2)、如图1，点P是第三象限内抛物线上的一个动点，当四边形 $A B P C$ 的面积最大时，求点 $P$ 的坐标；

(3)、如图2，线段 $A C$ 的垂直平分线交 $x$ 轴于点 $E$ ，垂足为 $D ， M$ 为抛物线的顶点，在直线 $D E$ 上是否存在一点 $G$ ，使 $△ C M G$ 的周长最小？若存在，求出点 $G$ 的坐标；若不存在，请说明理由．

查看试题解析

时间（小时）	0.5	1	1.5	2	2.5
人数（人）	12	22	10	5	3