湖南省张家界市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 2019的相反数是( )A、2019 B、-2019 C、 D、2. 为了有力回击美方单边主义贸易政策的霸凌行为,维护我国正当权益和世界多边贸易正常秩序,经国务院批准,决定于2019年6月1日起,对原产于美国的600亿美元进口商品加征关税,其中600亿美元用科学记数法表示为( )美元.A、 B、 C、 D、3. 下列四个立体图形中,其主视图是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、打开电视机,正在播放“张家界新闻”是必然事件 B、天气预报说“明天的降水概率为65%”,意味着明天一定下雨 C、两组数据平均数相同,则方差大的更稳定 D、数据5,6,7,7,8的中位数与众数均为76. 不等式组 的解集在数轴上表示为( )A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、打开电视机,正在播放“张家界新闻”是必然事件 B、天气预报说“明天的降水概率为65%”,意味着明天一定下雨 C、两组数据平均数相同,则方差大的更稳定 D、数据5,6,7,7,8的中位数与众数均为76. 不等式组 的解集在数轴上表示为( )A、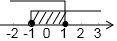 B、
B、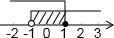 C、
C、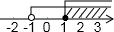 D、
D、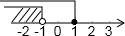 7. 如图,在 中, , , ,BD平分 ,则点D到AB的距离等于( )
7. 如图,在 中, , , ,BD平分 ,则点D到AB的距离等于( )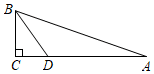 A、4 B、3 C、2 D、18. 如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转 后得到正方形 ,依此方式,绕点O连续旋转2019次得到正方形 ,那么点 的坐标是( )
A、4 B、3 C、2 D、18. 如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转 后得到正方形 ,依此方式,绕点O连续旋转2019次得到正方形 ,那么点 的坐标是( )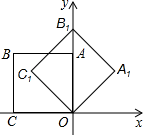 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 因式分解:x2y﹣y= .10. 已知直线 ,将一块含 角的直角三角板ABC按如图所示方式放置( ),并且顶点A , C分别落在直线a , b上,若 ,则 的度数是 .
 11. 为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况:
11. 为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况:捐书(本)
3
4
5
7
10
人数
5
7
10
11
7
该班学生平均每人捐书本.
12. 如图,在平面直角坐标系中,菱形OABC的顶点O为坐标原点,顶点A在x轴的正半轴上,顶点C在反比例函数 的图象上,已知菱形的周长是8, ,则k的值是 .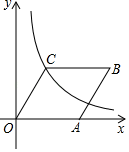 13. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多步.14. 如图:正方形ABCD的边长为1,点E , F分别为BC , CD边的中点,连接AE , BF交于点P , 连接PD , 则 .
13. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多步.14. 如图:正方形ABCD的边长为1,点E , F分别为BC , CD边的中点,连接AE , BF交于点P , 连接PD , 则 .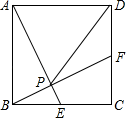
三、解答题
-
15. 计算: .16. 先化简,再求值: ,然后从0,1,2三个数中选择一个恰当的数代入求值.17. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G .
 (1)、求证: BF=CF ;
(1)、求证: BF=CF ;
(2)、若 , ,求FG的长.18. 某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.(1)、求购买甲、乙两种树苗各多少棵?(2)、为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?19. 阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为 ,排在第二位的数称为第二项,记为 ,依此类推,排在第n位的数称为第n项,记为 .所以,数列的一般形式可以写成: , , ,…, .
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,其中 , ,公差为 .
根据以上材料,解答下列问题:
(1)、等差数列5,10,15,…的公差d为 , 第5项是 .(2)、如果一个数列 , , ,…, …,是等差数列,且公差为d,那么根据定义可得到: , , ,…, ,….所以 ,
,
,
……,
由此,请你填空完成等差数列的通项公式: ()d.
(3)、 是不是等差数列 , , …的项?如果是,是第几项?20. 天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知 米, 米,AB与水平线 的夹角是 ,BC与水平线 的夹角是 .求:本次检修中,检修人员上升的垂直高度 是多少米?(结果精确到1米,参考数据: ) 21. 如图,AB为 的直径,且 ,点C是 上的一动点(不与A , B重合),过点B作 的切线交AC的延长线于点D , 点E是BD的中点,连接EC .
21. 如图,AB为 的直径,且 ,点C是 上的一动点(不与A , B重合),过点B作 的切线交AC的延长线于点D , 点E是BD的中点,连接EC .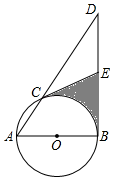 (1)、求证:EC是 的切线;(2)、当 时,求阴影部分面积.22. 为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)、求证:EC是 的切线;(2)、当 时,求阴影部分面积.22. 为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.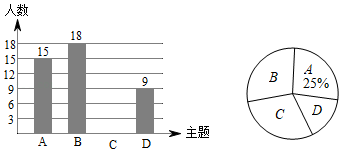 (1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“B”所在扇形的圆心角等于度;(4)、小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.23. 已知抛物线 过点 , 两点,与y轴交于点C , .
(1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“B”所在扇形的圆心角等于度;(4)、小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.23. 已知抛物线 过点 , 两点,与y轴交于点C , .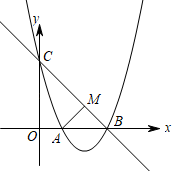 (1)、求抛物线的解析式及顶点D的坐标;(2)、过点A作 ,垂足为M , 求证:四边形ADBM为正方形;(3)、点P为抛物线在直线BC下方图形上的一动点,当 面积最大时,求点P的坐标;(4)、若点Q为线段OC上的一动点,问: 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
(1)、求抛物线的解析式及顶点D的坐标;(2)、过点A作 ,垂足为M , 求证:四边形ADBM为正方形;(3)、点P为抛物线在直线BC下方图形上的一动点,当 面积最大时,求点P的坐标;(4)、若点Q为线段OC上的一动点,问: 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.