湖南省湘西州2019年中考数学试卷
试卷更新日期：2019-08-06 类型：中考真卷
一、单选题
-
1. 下列运算中，正确的是（ ）A、2a+3a＝5a B、a6÷a3＝a2 C、（a﹣b）2＝a2﹣b2 D、2. 已知一个多边形的内角和是1080°，则这个多边形是（ ）A、五边形 B、六边形 C、七边形 D、八边形3. 下列立体图形中，主视图是圆的是（ ）A、
B、
C、
D、
4. 如图，直线a∥b，∠1＝50°，∠2＝40°，则∠3的度数为（ ）
A、40° B、90° C、50° D、100°5. 一元二次方程x2﹣2x+3＝0根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断6. 在平面直角坐标系中，将点（2，1）向右平移3个单位长度，则所得的点的坐标是（ ）
A、（0，5） B、（5，1） C、（2，4） D、（4，2）7. 下列四个图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
8. 从甲、乙、丙、丁四人中选一人参加射击比赛，经过三轮初赛，他们的平均成绩都是9环，方差分别是 ， ， ， ，你认为派谁去参赛更合适（ ）A、甲 B、乙 C、丙 D、丁9. 下列命题是真命题的是（ ）A、同旁内角相等，两直线平行 B、对角线互相平分的四边形是平行四边形 C、相等的两个角是对顶角 D、圆内接四边形对角相等10. 如图，在△ABC中，∠C＝90°，AC＝12，AB的垂直平分线EF交AC于点D，连接BD，若cos∠BDC＝ ，则BC的长是（ ）
A、10 B、8 C、4 D、2二、填空题
-
11. ﹣2019的相反数是 ．12. 要使二次根式 有意义，则x的取值范围为.13. 因式分解：ab﹣7a＝.14. 从﹣3,﹣1，π，0，3这五个数中随机抽取一个数，恰好是负数的概率是.15. 黔张常铁路将于2020年正式通车运营，这条铁路估算总投资36200000000元，数据36200000000用科学记数法表示为.16. 若关于x的方程3x﹣kx+2＝0的解为2，则k的值为.17. 下面是一个简单的数值运算程序，当输入x的值为16时，输出的数值为.（用科学计算器计算或笔算）.
18. 阅读材料：设 ＝（x1 ， y1）， ＝（x2 ， y2），如果 ∥ ，则x1•y2＝x2•y1 ， 根据该材料填空，已知 ＝（4，3）， ＝（8，m），且 ∥ ，则m＝.三、解答题
-
19. 计算： +2sin30°﹣（3.14﹣π）020. 解不等式组： 并把解集在数轴上表示出来.
21. 如图，在正方形ABCD中，点E，F分别在边CD，AD上，且AF＝CE.
(1)、求证：△ABF≌△CBE；(2)、若AB＝4，AF＝1，求四边形BEDF的面积.22. “扫黑除恶”受到广大人民的关注，某中学对部分学生就“扫黑除恶”知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：
(1)、接受问卷调查的学生共有人，扇形统计图中“很了解”部分所对应扇形的圆心角为；(2)、请补全条形统计图；(3)、若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.23. 如图，一次函数y＝kx+b的图象与反比例函数 的图象在第一象限交于点A（3，2），与y轴的负半轴交于点B，且OB＝4.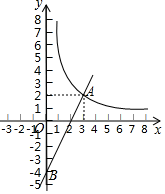
(1)、求函数 和y＝kx+b的解析式；(2)、结合图象直接写出不等式组0＜ ＜kx+b的解集.24. 列方程解应用题：某列车平均提速80km/h，用相同的时间，该列车提速前行驶300km，提速后比提速前多行驶200km，求该列车提速前的平均速度.25. 如图，△ABC内接于⊙O，AC＝BC，CD是⊙O的直径，与AB相交于点G，过点D作EF∥AB，分别交CA、CB的延长线于点E、F，连接BD.
(1)、求证：EF是⊙O的切线；(2)、求证：BD2＝AC•BF.26. 如图，抛物线y＝ax2+bx（a＞0）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C、D在抛物线上，∠BAD的平分线AM交BC于点M，点N是CD的中点，已知OA＝2，且OA：AD＝1：3.
(1)、求抛物线的解析式；(2)、F、G分别为x轴，y轴上的动点，顺次连接M、N、G、F构成四边形MNGF，求四边形MNGF周长的最小值；(3)、在x轴下方且在抛物线上是否存在点P，使△ODP中OD边上的高为 ？若存在，求出点P的坐标；若不存在，请说明理由；(4)、矩形ABCD不动，将抛物线向右平移，当平移后的抛物线与矩形的边有两个交点K、L，且直线KL平分矩形的面积时，求抛物线平移的距离.