湖南省湘潭市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 下列各数中是负数的是( )A、 B、﹣3 C、 D、2. 下列立体图形中,俯视图是三角形的是( )A、
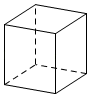 B、
B、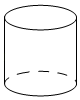 C、
C、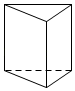 D、
D、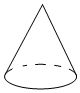 3. 今年某市参加初中学业水平考试的九年级学生人数约24000人,24000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于 的一元二次方程 有两个相等的实数根,则 ( )A、4 B、2 C、1 D、﹣46. 随着长株潭一体化进程不断推进,湘潭在交通方面越来越让人期待.将要实施的“两干一轨”项目中的“一轨”,是将长沙市地铁3号线南延至湘潭北站,往返长潭两地又将多“地铁”这一选择.为了解人们选择交通工具的意愿,随机抽取了部分市民进行调查,并根据调查结果绘制如下统计图,关于交通工具选择的人数数据,以下结论正确的是( )
3. 今年某市参加初中学业水平考试的九年级学生人数约24000人,24000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于 的一元二次方程 有两个相等的实数根,则 ( )A、4 B、2 C、1 D、﹣46. 随着长株潭一体化进程不断推进,湘潭在交通方面越来越让人期待.将要实施的“两干一轨”项目中的“一轨”,是将长沙市地铁3号线南延至湘潭北站,往返长潭两地又将多“地铁”这一选择.为了解人们选择交通工具的意愿,随机抽取了部分市民进行调查,并根据调查结果绘制如下统计图,关于交通工具选择的人数数据,以下结论正确的是( ) A、平均数是8 B、众数是11 C、中位数是2 D、极差是107. 如图,将 绕点 逆时针旋转70°到 的位置,若 ,则 ( )
A、平均数是8 B、众数是11 C、中位数是2 D、极差是107. 如图,将 绕点 逆时针旋转70°到 的位置,若 ,则 ( ) A、45° B、40° C、35° D、30°8. 现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,湘潭某家小型快递公司的分拣工小李和小江,在分拣同一类物件时,小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同,已知小李每小时比小江多分拣20个物件.若设小江每小时分拣 个物件,则可列方程为( )A、 B、 C、 D、
A、45° B、40° C、35° D、30°8. 现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,湘潭某家小型快递公司的分拣工小李和小江,在分拣同一类物件时,小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同,已知小李每小时比小江多分拣20个物件.若设小江每小时分拣 个物件,则可列方程为( )A、 B、 C、 D、二、填空题
-
9. 函数 中,自变量 的取值范围是 .10. 若 , ,则 .11. 为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是 .12. 计算: .13. 将一次函数 的图象向上平移2个单位,所得图象的函数表达式为 .14. 四边形的内角和为 .15. 如图,在四边形 中,若 ,则添加一个条件 , 能得到平行四边形 .(不添加辅助线,任意添加一个正确的条件即可)
 16. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积 (弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径 ⊥弦 时, 平分 )可以求解.现已知弦 米,半径等于5米的弧田,按照上述公式计算出弧田的面积为平方米.
16. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积 (弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径 ⊥弦 时, 平分 )可以求解.现已知弦 米,半径等于5米的弧田,按照上述公式计算出弧田的面积为平方米.
三、解答题
-
17. 解不等式组 ,并把它的解集在数轴上表示出来.
 18. 阅读材料:运用公式法分解因式,除了常用的平方差公式和完全平方公式以外,还可以应用其他公式,如立方和与立方差公式,其公式如下:
18. 阅读材料:运用公式法分解因式,除了常用的平方差公式和完全平方公式以外,还可以应用其他公式,如立方和与立方差公式,其公式如下:立方和公式: ;
立方差公式: ;
根据材料和已学知识,先化简,再求值: ,其中 .
19. 我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点 处垂直海面发射,当火箭到达点 处时,海岸边 处的雷达站测得点 到点 的距离为8千米,仰角为30°.火箭继续直线上升到达点 处,此时海岸边 处的雷达测得 处的仰角增加15°,求此时火箭所在点 处与发射站点 处的距离.(结果精确到0.1千米)(参考数据: , )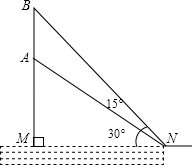 20. 每年5月份是心理健康宣传月,某中学开展以“关心他人,关爱自己”为主题的心理健康系列活动.为了解师生的心理健康状况,对全体2000名师生进行了心理测评,随机抽取20名师生的测评分数进行了以下数据的整理与分析:
20. 每年5月份是心理健康宣传月,某中学开展以“关心他人,关爱自己”为主题的心理健康系列活动.为了解师生的心理健康状况,对全体2000名师生进行了心理测评,随机抽取20名师生的测评分数进行了以下数据的整理与分析:①数据收集:抽取的20名师生测评分数如下
85,82,94,72,78,89,96,98,84,65,73,54,83,76,70,85,83,63,92,90.
②数据整理:将收集的数据进行分组并评价等第:
分数x
人数
5
a
5
2
1
等第
③数据分析:绘制成不完整的扇形统计图:

④依据统计信息回答问题
(1)、统计表中的 .(2)、心理测评等第 等的师生人数所占扇形的圆心角度数为 .(3)、学校决定对 等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?21. 如图,将 沿着 边翻折,得到 ,且 . (1)、判断四边形 的形状,并说明理由;(2)、若 , ,求四边形 的面积.22. 2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考(1)、“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)(2)、高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.23. 如图,在平面直角坐标系中,⊙ 与 轴的正半轴交于 两点,与 轴的正半轴相切于点 ,连接 ,已知⊙ 半径为2, ,双曲线 经过圆心 .
(1)、判断四边形 的形状,并说明理由;(2)、若 , ,求四边形 的面积.22. 2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考(1)、“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)(2)、高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.23. 如图,在平面直角坐标系中,⊙ 与 轴的正半轴交于 两点,与 轴的正半轴相切于点 ,连接 ,已知⊙ 半径为2, ,双曲线 经过圆心 . (1)、求双曲线 的解析式;(2)、求直线 的解析式.24. 某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店 两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.(1)、求该店平均每天销售这两种湘莲礼盒各多少盒?(2)、小亮调査发现, 种湘莲礼盒售价每降3元可多卖1盒.若 种湘莲礼盒的售价和销量不变,当 种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?25. 如图一,抛物线 过 三点
(1)、求双曲线 的解析式;(2)、求直线 的解析式.24. 某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店 两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.(1)、求该店平均每天销售这两种湘莲礼盒各多少盒?(2)、小亮调査发现, 种湘莲礼盒售价每降3元可多卖1盒.若 种湘莲礼盒的售价和销量不变,当 种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?25. 如图一,抛物线 过 三点 (1)、求该抛物线的解析式;(2)、 两点均在该抛物线上,若 ,求 点横坐标 的取值范围;(3)、如图二,过点 作 轴的平行线交抛物线于点 ,该抛物线的对称轴与 轴交于点 ,连结 ,点 为线段 的中点,点 分别为直线 和 上的动点,求 周长的最小值.26. 如图一,在射线 的一侧以 为一条边作矩形 , , ,点 是线段 上一动点(不与点 重合),连结 ,过点 作 的垂线交射线 于点 ,连接 .
(1)、求该抛物线的解析式;(2)、 两点均在该抛物线上,若 ,求 点横坐标 的取值范围;(3)、如图二,过点 作 轴的平行线交抛物线于点 ,该抛物线的对称轴与 轴交于点 ,连结 ,点 为线段 的中点,点 分别为直线 和 上的动点,求 周长的最小值.26. 如图一,在射线 的一侧以 为一条边作矩形 , , ,点 是线段 上一动点(不与点 重合),连结 ,过点 作 的垂线交射线 于点 ,连接 . (1)、求 的大小;(2)、问题探究:动点 在运动的过程中,
(1)、求 的大小;(2)、问题探究:动点 在运动的过程中,①是否能使 为等腰三角形,如果能,求出线段 的长度;如果不能,请说明理由.
② 的大小是否改变?若不改变,请求出 的大小;若改变,请说明理由.
(3)、问题解决:如图二,当动点 运动到 的中点时, 与 的交点为 , 的中点为 ,求线段 的长度.