湖南省衡阳市2019年中考数学试卷

试卷更新日期：2019-08-06 类型：中考真卷

进入出卷网下载

一、单选题

1. $- \frac{3}{4}$ 的相反数是（）

A、 $- \frac{3}{4}$ B、 $\frac{3}{4}$ C、 $- \frac{4}{3}$ D、 $\frac{4}{3}$

查看试题解析
2. 如果分式 $\frac{1}{x + 1}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \neq - 1$ B、 $x > - 1$ C、全体实数 D、 $x = - 1$

查看试题解析
3. 2018年6月14日，探月工程嫦娥四号任务“鹊桥”中继星成功实施轨道捕获控制，进入环绕距月球65000公里的地月拉格朗日L2点Halo使命轨道，成为世界首颗运行在地月L2点Halo轨道的卫星，用科学记数法表示65000公里为（）公里．

A、 $0.65 \times 10^{5}$ B、 $65 \times 10^{3}$ C、 $6.5 \times 10^{4}$ D、 $6.5 \times 10^{5}$

查看试题解析
4. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列各式中，计算正确的是（）

A、 $8 a - 3 b = 5 a b$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{8} \div a^{4} = a^{2}$ D、 $a^{2} \cdot a = a^{3}$

查看试题解析
6. 如图，已知 $A B ∕ ∕ C D$ ， $A F$ 交 $C D$ 于点 $E$ ，且 $B E ⊥ A F ， ∠ B E D = 40 °$ ，则 $∠ A$ 的度数是（）

A、 $40 °$ B、 $50 °$ C、 $80 °$ D、 $90 °$

查看试题解析
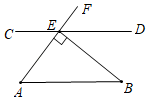7. 某校5名同学在“国学经典颂读”比赛中，成绩（单位：分）分别是86，95，97，90，88，这组数据的中位数是（）

A、97 B、90 C、95 D、88

查看试题解析
8. 下列命题是假命题的是（）

A、 $n$ 边形（ $n \geq 3$ ）的外角和是 $360 °$ B、线段垂直平分线上的点到线段两个端点的距离相等 C、相等的角是对顶角 D、矩形的对角线互相平分且相等

查看试题解析
9. 不等式组 ${\begin{array}{l} 2 x > 3 x \\ x + 4 > 2 \end{array}$ 的整数解是（）

A、0 B、 $- 1$ C、 $- 2$ D、1

查看试题解析
10. 国家实施”精准扶贫“政策以来，很多贫困人口走向了致富的道路．某地区2016年底有贫困人口9万人，通过社会各界的努力，2018年底贫困人口减少至1万人．设2016年底至2018年底该地区贫困人口的年平均下降率为 $x$ ，根据题意列方程得（）

A、 $9 (1 - 2 x) = 1$ B、 $9 {(1 - x)}^{2} = 1$ C、 $9 (1 + 2 x) = 1$ D、 $9 {(1 + x)}^{2} = 1$

查看试题解析
11. 如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ （ $m$ 为常数且 $m \neq 0$ ）的图象都经过 $A (- 1 ， 2) ， B (2 ， - 1)$ ，结合图象，则不等式 $\frac{k}{x}$ 的解集是（）

A、 $x < - 1$ B、 $- 1 < x < 0$ C、 $x < - 1$ 或 $0 < x < 2$ D、 $- 1 < x < 0$ 或 $x > 2$

查看试题解析
12. 如图，在直角三角形 $A B C$ 中， $∠ C = 90 ° ， A C = B C$ ， $E$ 是 $A B$ 的中点，过点 $E$ 作 $A C$ 和 $B C$ 的垂线，垂足分别为点 $D$ 和点 $F$ ，四边形 $C D E F$ 沿着 $C A$ 方向匀速运动，点 $C$ 与点 $A$ 重合时停止运动，设运动时间为 $t$ ，运动过程中四边形 $C D E F$ 与 $Δ A B C$ 的重叠部分面积为 $S$ ．则 $S$ 关于 $t$ 的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

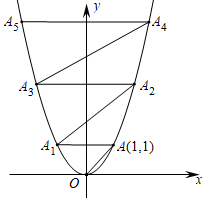
13. 因式分解：2a²﹣8= ．

查看试题解析
14. 在一个不透明布袋里装有3个白球、2个红球和 $a$ 个黄球，这些球除颜色不同其它没有任何区别．若从该布袋里任意摸出1个球，该球是黄球的概率为 $\frac{1}{2}$ ，则 $a$ 等于．

查看试题解析
15. 计算： $\sqrt{27} - \sqrt{3}$ =.

查看试题解析
16. 计算： $\frac{x}{x - 1}$ + $\frac{1}{1 - x}$ = ．

查看试题解析
17. 已知圆的半径是6，则圆内接正三角形的边长是．

查看试题解析
18. 在平面直角坐标系中，抛物线 $y = x^{2}$ 的图象如图所示．已知 $A$ 点坐标为 $(1 ， 1)$ ，过点 $A$ 作 $A A_{1} ∕ ∕ x$ 轴交抛物线于点 $A_{1}$ ，过点 $A_{1}$ 作 $A_{1} A_{2} ∕ ∕ O A$ 交抛物线于点 $A_{2}$ ，过点 $A_{2}$ 作 $A_{2} A_{3} ∕ ∕ x$ 轴交抛物线于点 $A_{3}$ ，过点 $A_{3}$ 作 $A_{3} A_{4} ∕ ∕ O A$ 交抛物线于点 $A_{4}$ ……，依次进行下去，则点 $A_{2019}$ 的坐标为．

查看试题解析

三、解答题

19. ${(\frac{1}{2})}^{- 3} + | \sqrt{3} - 2 | + \tan 60 ° - {(- 2019)}^{0}$

查看试题解析
20. 进行了统计，并绘制了如下两幅不完整的统计图．请结合统计图中的信息解决下列问题：

(1)、这次学校抽查的学生人数是；

(2)、将条形统计图补充完整；

(3)、如果该校共有1000名学生，请你估计该校报 $D$ 的学生约有多少人？

查看试题解析
21. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析
22. 如图，在一次综合实践活动中，小亮要测量一楼房的高度，先在坡面 $D$ 处测得楼房顶部A的仰角为 $30 °$ ，沿坡面向下走到坡脚 $C$ 处，然后向楼房方向继续行走10米到达 $E$ 处，测得楼房顶部 $A$ 的仰角为 $60 °$ ．已知坡面 $C D = 10$ 米，山坡的坡度 $i = 1 ： \sqrt{3}$ （坡度 $i$ 是指坡面的铅直高度与水平宽度的比），求楼房 $A B$ 高度．（结果精确到0.1米）（参考数据： $\sqrt{3} \approx 1.73$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
23. 如图，点 $A 、 B 、 C$ 在半径为8的 $⊙ O$ 上，过点 $B$ 作 $B D ∕ ∕ A C$ ，交 $O A$ 延长线于点 $D$ ．连接 $B C$ ，且 $∠ B C A = ∠ O A C = 30 °$ ．

(1)、求证： $B D$ 是 $⊙ O$ 的切线；

(2)、求图中阴影部分的面积．

查看试题解析
24. 某商店购进 $A$ 、 $B$ 两种商品，购买1个 $A$ 商品比购买1个 $B$ 商品多花10元，并且花费300元购买 $A$ 商品和花费100元购买 $B$ 商品的数量相等．

(1)、求购买一个 $A$ 商品和一个 $B$ 商品各需要多少元；

(2)、商店准备购买 $A$ 、 $B$ 两种商品共80个，若 $A$ 商品的数量不少于 $B$ 商品数量的4倍，并且购买 $A$ 、 $B$ 商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？

查看试题解析
25. 如图，二次函数 $y = x^{2} + b x + c$ 的图象与 $x$ 轴交于点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，与 $y$ 轴交于点 $N$ ，以 $A B$ 为边在 $x$ 轴上方作正方形 $A B C D$ ，点 $P$ 是 $x$ 轴上一动点，连接 $C P$ ，过点 $P$ 作 $C P$ 的垂线与 $y$ 轴交于点 $E$ ．

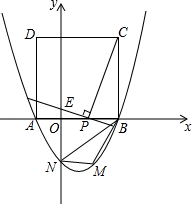(1)、求该抛物线的函数关系表达式；

(2)、当点 $P$ 在线段 $O B$ （点 $P$ 不与 $O 、 B$ 重合）上运动至何处时，线段 $O E$ 的长有最大值？并求出这个最大值；

(3)、在第四象限的抛物线上任取一点 $M$ ，连接 $M N 、 M B$ ．请问： $Δ M B N$ 的面积是否存在最大值？若存在，求出此时点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析
26. 如图，在等边 $Δ A B C$ 中， $A B = 6 c m$ ，动点 $P$ 从点 $A$ 出发以 $1 c m / s$ 的速度沿 $A B$ 匀速运动．动点 $Q$ 同时从点 $C$ 出发以同样的速度沿 $B C$ 的延长线方向匀速运动，当点 $P$ 到达点 $B$ 时，点 $P 、 Q$ 同时停止运动．设运动时间为以 $t (s)$ ．过点 $P$ 作 $P E ⊥ A C$ 于 $E$ ，连接 $P Q$ 交 $A C$ 边于 $D$ ．以 $C Q 、 C E$ 为边作平行四边形 $C Q F E$ ．

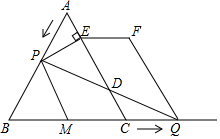(1)、当 $t$ 为何值时， $Δ B P Q$ 为直角三角形；

(2)、是否存在某一时刻 $t$ ，使点 $F$ 在 $∠ A B C$ 的平分线上？若存在，求出 $t$ 的值，若不存在，请说明理由；

(3)、求 $D E$ 的长；

(4)、取线段BC的中点M ，连接PM ，将△BMP 沿直线PM 翻折，得△B^' PM ，连接AB^' ，当t为何值时， AB^' 的值最小？并求出最小值．

查看试题解析