湖南省郴州市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 如图,数轴上表示 的相反数的点是( )
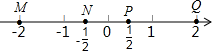 A、M B、N C、P D、Q2. 如图是我国几家银行的标志,其中既是轴对称图形又是中心对称图形的是( )A、
A、M B、N C、P D、Q2. 如图是我国几家银行的标志,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 邓小平曾说:“中东有石油,中国有稀土”.稀土是加工制造国防、军工等工业品不可或缺的原料.据有关统计数据表明:至2017年止,我国已探明稀土储量约4400万吨,居世界第一位,请用科学记数法表示44000000为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根6. 下列采用的调查方式中,合适的是( )A、为了解东江湖的水质情况,采用抽样调查的方式 B、我市某企业为了解所生产的产品的合格率,采用普查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查,采用抽样调查的方式 D、某市教育部门为了解该市中小学生的视力情况,采用普查的方式7. 如图,分别以线段AB的两端点A,B为圆心,大于 AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是( )
3. 邓小平曾说:“中东有石油,中国有稀土”.稀土是加工制造国防、军工等工业品不可或缺的原料.据有关统计数据表明:至2017年止,我国已探明稀土储量约4400万吨,居世界第一位,请用科学记数法表示44000000为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根6. 下列采用的调查方式中,合适的是( )A、为了解东江湖的水质情况,采用抽样调查的方式 B、我市某企业为了解所生产的产品的合格率,采用普查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查,采用抽样调查的方式 D、某市教育部门为了解该市中小学生的视力情况,采用普查的方式7. 如图,分别以线段AB的两端点A,B为圆心,大于 AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是( )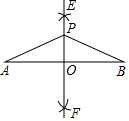 A、 B、 C、 D、8. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形ADOF的边长是( )
A、 B、 C、 D、8. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形ADOF的边长是( )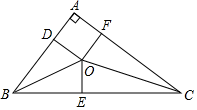 A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
9. 二次根式 中,x的取值范围是 .10. 若 ,则 .11. 如图,直线a,b被直线c,d所截.若 , , ,则 的度数为度.
 12. 某校举行演讲比赛,七个评委对小明的打分如下:9,8,7,6,9,9,7,这组数据的中位数是 .13. 某商店今年6月初销售纯净水的数量如下表所示:
12. 某校举行演讲比赛,七个评委对小明的打分如下:9,8,7,6,9,9,7,这组数据的中位数是 .13. 某商店今年6月初销售纯净水的数量如下表所示:日期
1
2
3
4
数量(瓶)
120
125
130
135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为瓶.
14. 如图是甲、乙两人6次投篮测试(每次投篮10个)成绩的统计图,甲、乙两人测试成绩的方差分别记作 、 ,则 .(填“>”,“=”或“<”) 15. 已知某几何体的三视图如图,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 . (结果保留π)
15. 已知某几何体的三视图如图,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 . (结果保留π) 16. 如图,点A,C分别是正比例函数 的图象与反比例函数 的图象的交点,过A点作 轴于点D,过C点作 轴于点B,则四边形ABCD的面积为 .
16. 如图,点A,C分别是正比例函数 的图象与反比例函数 的图象的交点,过A点作 轴于点D,过C点作 轴于点B,则四边形ABCD的面积为 .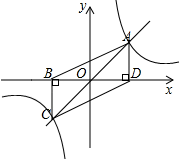
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 如图, 中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.求证:四边形ACDF是平行四边形.
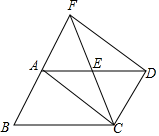 20. 某市去年成功举办2018郴州国际休闲旅游文化节,获评“全国森林旅游示范市”.某市有A,B,C,D,E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图:
20. 某市去年成功举办2018郴州国际休闲旅游文化节,获评“全国森林旅游示范市”.某市有A,B,C,D,E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图: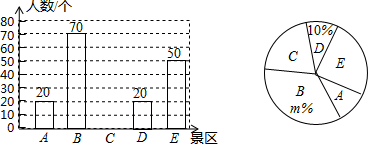 (1)、该小区居民在这次随机调查中被调查到的人数是人, , 并补全条形统计图;(2)、若该小区有居民1200人,试估计去B地旅游的居民约有多少人?(3)、小军同学已去过E地旅游,暑假期间计划与父母从A,B,C,D四个景区中,任选两个去旅游,求选到A,C两个景区的概率.(要求画树状图或列表求概率)21. 如图所示,巡逻船在A处测得灯塔C在北偏东 方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东 方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km.参考数据: , , )
(1)、该小区居民在这次随机调查中被调查到的人数是人, , 并补全条形统计图;(2)、若该小区有居民1200人,试估计去B地旅游的居民约有多少人?(3)、小军同学已去过E地旅游,暑假期间计划与父母从A,B,C,D四个景区中,任选两个去旅游,求选到A,C两个景区的概率.(要求画树状图或列表求概率)21. 如图所示,巡逻船在A处测得灯塔C在北偏东 方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东 方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km.参考数据: , , )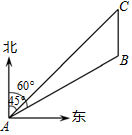 22. 某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.(1)、每台A,B两种型号的机器每小时分别加工多少个零件?(2)、如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?23. 如图,已知AB是 的直径,CD与 相切于点D,且 .
22. 某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.(1)、每台A,B两种型号的机器每小时分别加工多少个零件?(2)、如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?23. 如图,已知AB是 的直径,CD与 相切于点D,且 . (1)、求证:BC是 的切线;(2)、延长CO交 于点 E.若 ,⊙O的半径为2,求 的长.(结果保留π)24. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:
(1)、求证:BC是 的切线;(2)、延长CO交 于点 E.若 ,⊙O的半径为2,求 的长.(结果保留π)24. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:x
…
0
1
2
3
…
y
…
1
2
1
0
1
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
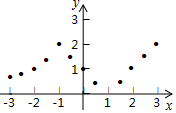 (1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;(2)、研究函数并结合图象与表格,回答下列问题:
(1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;(2)、研究函数并结合图象与表格,回答下列问题:①点 , , , 在函数图象上, , ;(填“>”,“=”或“<”)
②当函数值 时,求自变量x的值;
③在直线 的右侧的函数图象上有两个不同的点 , ,且 ,求 的值;
④若直线 与函数图象有三个不同的交点,求a的取值范围.