黑龙江省伊春市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 下列各运算中,计算正确的是( )A、 B、 C、 D、2. 下列图形是我国国产品牌汽车的标识,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是( )
3. 如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是( ) A、 B、 C、 D、4. 某班在阳光体育活动中,测试了五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据.在统计时,出现了一处不符合题意:将最低成绩写得更低了,则计算结果不受影响的是( )A、平均数 B、中位数 C、方差 D、极差5. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是 ,则这种植物每个支干长出的小分支个数是( )A、 B、 C、 D、6. 如图,在平面直角坐标系中,点 为坐标原点,平行四边形 的顶点 在反比例函数 上,顶点 在反比例函数 上,点 在 轴的正半轴上,则平行四边形 的面积是( )
A、 B、 C、 D、4. 某班在阳光体育活动中,测试了五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据.在统计时,出现了一处不符合题意:将最低成绩写得更低了,则计算结果不受影响的是( )A、平均数 B、中位数 C、方差 D、极差5. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是 ,则这种植物每个支干长出的小分支个数是( )A、 B、 C、 D、6. 如图,在平面直角坐标系中,点 为坐标原点,平行四边形 的顶点 在反比例函数 上,顶点 在反比例函数 上,点 在 轴的正半轴上,则平行四边形 的面积是( ) A、 B、 C、 D、7. 已知关于 的分式方程 的解是非正数,则 的取值范围是( )A、 B、 C、 D、8. 如图,矩形 的对角线 、 相交于点 , ,过点 作 ,过点 作 , 、 交于点 ,连接 ,则 ( )
A、 B、 C、 D、7. 已知关于 的分式方程 的解是非正数,则 的取值范围是( )A、 B、 C、 D、8. 如图,矩形 的对角线 、 相交于点 , ,过点 作 ,过点 作 , 、 交于点 ,连接 ,则 ( )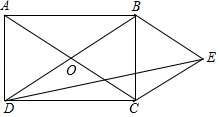 A、 B、 C、 D、9. 如图,在平行四边形 中, , ,过点 作边 的垂线 交 的延长线于点 ,点 是垂足,连接 、 , 交 于点 .则下列结论:①四边形 是正方形;② ;③ ;④ ,正确的个数是( )
A、 B、 C、 D、9. 如图,在平行四边形 中, , ,过点 作边 的垂线 交 的延长线于点 ,点 是垂足,连接 、 , 交 于点 .则下列结论:①四边形 是正方形;② ;③ ;④ ,正确的个数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 中国政府提出的“一带一路”倡议,近两年来为沿线国家创造了约 个就业岗位.将数据 用科学记数法表示为 .11. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .12. 如图,在四边形 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使四边形 是平行四边形.
 13. 在不透明的甲、乙两个盒子中装有除颜色外完全相同的小球,甲盒中有 个白球、 个黄球,乙盒中有 个白球、 个黄球,分别从每个盒中随机摸出 个球,则摸出的 个球都是黄球的概率是 .14. 若关于 的一元一次不等式组 的解集为 ,则 的取值范围是 .15. 如图,在⊙ 中,半径 垂直于弦 ,点 在圆上且 ,则 的度数为 .
13. 在不透明的甲、乙两个盒子中装有除颜色外完全相同的小球,甲盒中有 个白球、 个黄球,乙盒中有 个白球、 个黄球,分别从每个盒中随机摸出 个球,则摸出的 个球都是黄球的概率是 .14. 若关于 的一元一次不等式组 的解集为 ,则 的取值范围是 .15. 如图,在⊙ 中,半径 垂直于弦 ,点 在圆上且 ,则 的度数为 .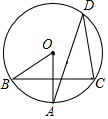 16. 若一个圆锥的底面圆的周长是 cm,母线长是 ,则该圆锥的侧面展开图的圆心角度数是 .17. 如图,矩形 中, , ,点 是矩形 内一动点,且 ,则 的最小值为 .
16. 若一个圆锥的底面圆的周长是 cm,母线长是 ,则该圆锥的侧面展开图的圆心角度数是 .17. 如图,矩形 中, , ,点 是矩形 内一动点,且 ,则 的最小值为 . 18. 一张直角三角形纸片 , , , ,点 为 边上的任一点,沿过点 的直线折叠,使直角顶点 落在斜边 上的点 处,当 是直角三角形时,则 的长为 .19. 如图,四边形 是边长为 的正方形,以对角线 为边作第二个正方形 ,连接 ,得到 ;再以对角线 为边作第三个正方形 ,连接 ,得到 ;再以对角线 为边作第四个正方形,连接 ,得到 ……记 、 、 的面积分别为 、 、 ,如此下去,则 .
18. 一张直角三角形纸片 , , , ,点 为 边上的任一点,沿过点 的直线折叠,使直角顶点 落在斜边 上的点 处,当 是直角三角形时,则 的长为 .19. 如图,四边形 是边长为 的正方形,以对角线 为边作第二个正方形 ,连接 ,得到 ;再以对角线 为边作第三个正方形 ,连接 ,得到 ;再以对角线 为边作第四个正方形,连接 ,得到 ……记 、 、 的面积分别为 、 、 ,如此下去,则 .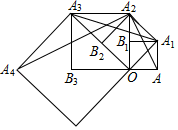 20. 某学校计划用 件同样的奖品全部用于奖励在“经典诵读”活动中表现突出的班级,一等奖奖励 件,二等奖奖励 件,则分配一、二等奖个数的方案有( )A、 种 B、 种 C、 种 D、 种
20. 某学校计划用 件同样的奖品全部用于奖励在“经典诵读”活动中表现突出的班级,一等奖奖励 件,二等奖奖励 件,则分配一、二等奖个数的方案有( )A、 种 B、 种 C、 种 D、 种三、解答题
-
21. 先化简,再求值: ,期中 .22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上.
 (1)、画出 关于 轴对称的 ,并写出点 的坐标;(2)、画出 绕原点 顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求线段 在旋转过程中扫过的面积(结果保留 ).23. 如图,在平面直角坐标系中,抛物线 与 轴交于点 、点 ,与 轴交于点 .
(1)、画出 关于 轴对称的 ,并写出点 的坐标;(2)、画出 绕原点 顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求线段 在旋转过程中扫过的面积(结果保留 ).23. 如图,在平面直角坐标系中,抛物线 与 轴交于点 、点 ,与 轴交于点 .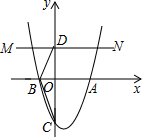 (1)、求拋物线的解析式;(2)、过点 作直线 轴,点 在直线 上且 ,直接写出点 的坐标.24. “世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)、求拋物线的解析式;(2)、过点 作直线 轴,点 在直线 上且 ,直接写出点 的坐标.24. “世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题: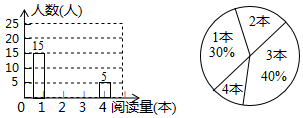 (1)、求本次调查中共抽取的学生人数;(2)、补全条形统计图;(3)、在扇形统计图中,阅读 本书籍的人数所在扇形的圆心角度数是;(4)、若该校有 名学生,估计该校在这次活动中阅读书籍的数量不低于 本的学生有多少人?25. 小明放学后从学校回家,出发 分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发 分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程 (米)与小强所用时间 (分钟)之间的函数图象如图所示.
(1)、求本次调查中共抽取的学生人数;(2)、补全条形统计图;(3)、在扇形统计图中,阅读 本书籍的人数所在扇形的圆心角度数是;(4)、若该校有 名学生,估计该校在这次活动中阅读书籍的数量不低于 本的学生有多少人?25. 小明放学后从学校回家,出发 分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发 分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程 (米)与小强所用时间 (分钟)之间的函数图象如图所示. (1)、求函数图象中 的值;(2)、求小强的速度;(3)、求线段 的函数解析式,并写出自变量的取值范围.26. 如图,在 中, , 于点 , 于点 , 与 交于点 , 于点 ,点 是 的中点,连接 并延长交 于点 .
(1)、求函数图象中 的值;(2)、求小强的速度;(3)、求线段 的函数解析式,并写出自变量的取值范围.26. 如图,在 中, , 于点 , 于点 , 与 交于点 , 于点 ,点 是 的中点,连接 并延长交 于点 . (1)、如图①所示,若 ,求证: ;(2)、如图②所示,若 ,如图③所示,若 (点 与点 重合),猜想线段 、 与 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.27. 为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买 个甲种文具、 个乙种文具共需花费 元;购买 个甲种文具、 个乙种文具共需花费 元.(1)、求购买一个甲种文具、一个乙种文具各需多少元?(2)、若学校计划购买这两种文具共 个,投入资金不少于 元又不多于 元,设购买甲种文具 个,求有多少种购买方案?(3)、设学校投入资金 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?28. 如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒 个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)、如图①所示,若 ,求证: ;(2)、如图②所示,若 ,如图③所示,若 (点 与点 重合),猜想线段 、 与 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.27. 为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买 个甲种文具、 个乙种文具共需花费 元;购买 个甲种文具、 个乙种文具共需花费 元.(1)、求购买一个甲种文具、一个乙种文具各需多少元?(2)、若学校计划购买这两种文具共 个,投入资金不少于 元又不多于 元,设购买甲种文具 个,求有多少种购买方案?(3)、设学校投入资金 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?28. 如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒 个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .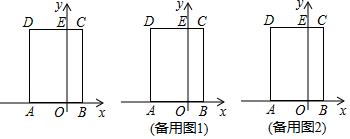 (1)、求点 的坐标;(2)、求 关于 的函数关系式,并写出自变量的取值范围;(3)、在点 的运动过程中,是否存在 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.
(1)、求点 的坐标;(2)、求 关于 的函数关系式,并写出自变量的取值范围;(3)、在点 的运动过程中,是否存在 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.