广东省广州市2019年中考数学试卷

试卷更新日期：2019-08-06 类型：中考真卷

进入出卷网下载

一、单选题

1. $| - 6 |$ =（）

A、-6 B、6 C、 $- \frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 广州正稳步推进碧道建设，营造“水清岸绿、鱼翔浅底、水草丰美、白鹭成群”的生态廊道，使之成为老百姓美好生活的好去处，到今年底各区完成碧道试点建设的长度分别为（单位：千米）：5，5.2，5，5，5，6.4，6，5，6.68，48.4，6.3，这组数据的众数是（）

A、5 B、5.2 C、6 D、6.4

查看试题解析
3. 如图，有一斜坡AB，坡顶B离地面的高度BC为30m，斜坡的倾斜角是∠BAC，若 $\tan ∠ B A C = \frac{2}{5}$ ，则次斜坡的水平距离AC为（）

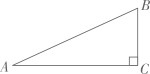A、75m B、50m C、30m D、12m

查看试题解析
4. 下列运算正确的是（）

A、－3－2＝－1 B、 $3 \times {(- \frac{1}{3})}^{2} = - \frac{1}{3}$ C、 $x^{3} \cdot x^{5} = x^{15}$ D、 $\sqrt{a} \cdot \sqrt{a b} = a \sqrt{b}$

查看试题解析
5. 平面内，⊙O的半径为1，点P到O的距离为2，过点P可作⊙O的切线条数为（）

A、0条 B、1条 C、2条 D、无数条

查看试题解析
6. 甲、乙二人做某种机械零件，已知每小时甲比乙少做8个，甲做120个所用的时间与乙做150个所用的时间相等，设甲每小时做x个零件，下列方程正确的是（）

A、 $\frac{120}{x} = \frac{150}{x - 8}$ B、 $\frac{120}{x + 8} = \frac{150}{x}$ C、 $\frac{120}{x - 8} = \frac{150}{x}$ D、 $\frac{120}{x} = \frac{150}{x + 8}$

查看试题解析
7. 如图，平行四边形ABCD中，AB=2，AD=4，对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点，则下列说法正确的是（）

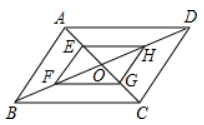A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 $Δ A B O$ 的面积是 $Δ E F O$ 的面积的2倍

查看试题解析
8. 若点 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (3 ， y_{3})$ 在反比例函数 $y = \frac{6}{x}$ 的图像上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{2} < y_{1}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{1} < y_{2} < y_{3}$

查看试题解析
9. 如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE=3，AF=5，则AC的长为（）

A、 $4 \sqrt{5}$ B、 $4 \sqrt{3}$ C、10 D、8

查看试题解析
10. 关于x的一元二次方程 $x^{2} - (k - 1) x - k + 2 = 0$ 有两个实数根 $x_{1}, x_{2}$ ， $(x_{1} - x_{2} + 2) (x_{1} - x_{2} - 2) + 2 x_{1} x_{2}$ $= - 3$ ，则k的值（）

A、0或2 B、-2或2 C、-2 D、2

查看试题解析

二、填空题

11. 如图，点A，B，C在直线l上，PB⊥l ， PA=6cm，PB=5cm，PC=7cm，则点P到直线l的距离是cm.

查看试题解析
12. 代数式 $\frac{1}{\sqrt{x - 8}}$ 有意义时，x应满足的条件是.

查看试题解析
13. 分解因式：x²y+2xy+y= ．

查看试题解析
14. 一副三角板如图放置，将三角板ADE绕点A逆时针旋转 $α (0^{\circ} < α < 90^{\circ})$ ，使得三角板ADE的一边所在的直线与BC垂直，则 $α$ 的度数为.

查看试题解析
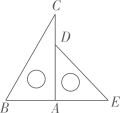15. 如图放置的一个圆锥，它的主视图是直角边长为2的等腰直角三角形，则该圆锥侧面展开扇形的弧长为.（结果保留π）

查看试题解析
16. 如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM=45°，点F在射线AM上，且 $A F = \sqrt{2} B E$ ，CF与AD相交于点G，连接EC，EF，EG，则下列结论：①∠ECF=45°；② $Δ A E G$ 的周长为 $(1 + \frac{\sqrt{2}}{2}) a$ ；③ $B E^{2} + D G^{2} = E G^{2}$ ；④ $Δ E A F$ 的面积的最大值 $\frac{1}{8} a^{2}$ .其中正确的结论是.（填写所有正确结论的序号）

查看试题解析

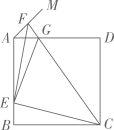
三、解答题

17. 解方程组： ${\begin{array}{l} x - y = 1 \\ x + 3 y = 9 \end{array}$

查看试题解析
18. 如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证： $Δ A D E ≅ C F E$

查看试题解析
19. 已知 $P = \frac{2 a}{a^{2} - b^{2}} - \frac{1}{a + b} (a \neq \pm b)$

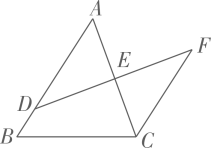(1)、化简P；

(2)、若点（a ， b）在一次函数 $y = x - \sqrt{2}$ 的图像上，求P的值。

查看试题解析

20. 某中学抽取了40名学生参加“平均每周课外阅读时间”的调查，由调查结果绘制了如下不完整的频数分布表和扇形统计图.

组别	时间/小时	频数/人数
A组	$0 \leq t < 1$	2
B组	$1 \leq t < 2$	m
C组	$2 \leq t < 3$	10
D组	$3 \leq t < 4$	12
E组	$4 \leq t < 5$	7
F组	$t \geq 5$	4

频数分布表

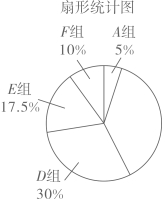
请根据图表中的信息解答下列问题：

(1)、求频数分布表中m的值；

(2)、求B组，C组在扇形统计图中分别对应扇形的圆心角度数，并补全扇形统计图；

(3)、已知F组的学生中，只有1名男生，其余都是女生，用列举法求以下事件的概率：从F组中随机选取2名学生，恰好都是女生。

查看试题解析

21. 随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业，据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座。

(1)、计划到2020年底，全省5G基站的数量是多少万座？；

(2)、按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率。

查看试题解析
22. 如图，在平面直角坐标系xOy中，菱形ABCD的对角线AC与BD交于点P（-1，2），AB⊥x轴于点E，正比例函数y=mx的图像与反比例函数 $y = \frac{n - 3}{x}$ 的图像相交于A，P两点。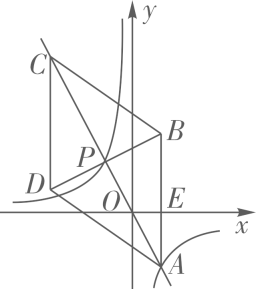

(1)、求m，n的值与点A的坐标；

(2)、求证： $Δ C P D$ ∽ $Δ A E O$

(3)、求 $\sin ∠ C D B$ 的值

查看试题解析
23. 如图，⊙O的直径AB=10，弦AC=8，连接BC。

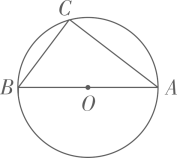(1)、尺规作图：作弦CD，使CD=BC（点D不与B重合），连接AD；（保留作图痕迹，不写作法）

(2)、在（1）所作的图中，求四边形ABCD的周长。

查看试题解析
24. 如图，等边 $Δ A B C$ 中，AB=6，点D在BC上，BD=4，点E为边AC上一动点（不与点C重合）， $Δ C D E$ 关于DE的轴对称图形为 $Δ F D E$ .

(1)、当点F在AC上时，求证：DF//AB；

(2)、设 $Δ A C D$ 的面积为S₁ ， $Δ A B F$ 的面积为S₂ ，记S=S₁-S₂ ， S是否存在最大值？若存在，求出S的最大值；若不存在，请说明理由；

(3)、当B，F，E三点共线时。求AE的长。

查看试题解析
25. 已知抛物线G： $y = m x^{2} - 2 m x - 3$ 有最低点。

(1)、求二次函数 $y = m x^{2} - 2 m x - 3$ 的最小值（用含m的式子表示）；

(2)、将抛物线G向右平移m个单位得到抛物线G₁_。经过探究发现，随着m的变化，抛物线G₁顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；

(3)、记（2）所求的函数为H，抛物线G与函数H的图像交于点P，结合图像，求点P的纵坐标的取值范围.

查看试题解析