内蒙古鄂尔多斯市2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 有理数 的相反数为( )A、﹣3 B、 C、 D、32. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
 A、
A、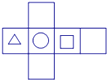 B、
B、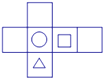 C、
C、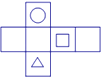 D、
D、 3. 禽流感病毒的半径大约是0.00000045米,它的直径用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米4. 如图,在正方形 的外侧,作等边 ,则 为( )
3. 禽流感病毒的半径大约是0.00000045米,它的直径用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米4. 如图,在正方形 的外侧,作等边 ,则 为( )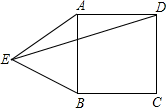 A、15° B、35° C、45° D、55°5. 下列计算
A、15° B、35° C、45° D、55°5. 下列计算① ② ③ ④ ⑤ ,
其中任意抽取一个,运算结果正确的概率是( )
A、 B、 C、 D、6. 下表是抽查的某班10名同学中考体育测试成绩线计表.成绩(分)
30
25
20
15
人数(人)
2
1
若成绩的平均数为23,中位数是 ,众数是 ,则a-b的值是( )
A、﹣5 B、﹣2.5 C、2.5 D、57. 如图,在 中, ,依据尺规作图的痕迹,计算 的度数是( )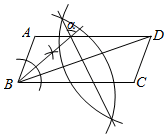 A、67°29′ B、67°9′ C、66°29′ D、66°9′8. 下列说法正确的是( )
A、67°29′ B、67°9′ C、66°29′ D、66°9′8. 下列说法正确的是( )①函数 中自变量 的取值范围是 .②若等腰三角形的两边长分别为3和7,则第三边长是3或7.③一个正六边形的内角和是其外角和的2倍.④同旁内角互补是真命题.⑤关于 的一元二次方程 有两个不相等的实数根.
A、①②③ B、①④⑤ C、②④ D、③⑤9. 如图,矩形 与菱形 的对角线均交于点 ,且 ,将矩形折叠,使点 与点 重合,折痕 过点 .若 , , ,则 的长为( ) A、 B、 C、 D、10. 在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从 两地同时出发,相向而行.快车到达 地后,停留3秒卸货,然后原路返回 地,慢车到达 地即停运休息,如图表示的是两车之间的距离 (米)与行驶时间 (秒)的函数图象,根据图象信息,计算 的值分别为( )
A、 B、 C、 D、10. 在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从 两地同时出发,相向而行.快车到达 地后,停留3秒卸货,然后原路返回 地,慢车到达 地即停运休息,如图表示的是两车之间的距离 (米)与行驶时间 (秒)的函数图象,根据图象信息,计算 的值分别为( )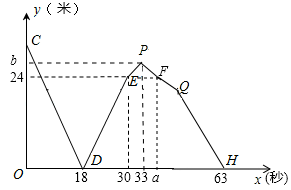 A、39,26 B、39,26.4 C、38,26 D、38,26.4
A、39,26 B、39,26.4 C、38,26 D、38,26.4二、填空题
-
11. 计算: .12. 一组数据﹣1,0,1,2,3的方差是 .13. 如图, 中, ,以 为直径的⊙ 分别与 , 交于点 ,连接 ,过点 作 于点 .若 , ,则阴影部分的面积是 .
 14. 如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若 是“好玩三角形”,且 ,则 .15. 如图,有一条折线 ,它是由过 , , 组成的折线依次平移8,16,24,…个单位得到的,直线 与此折线有 ( 且为整数)个交点,则 的值为 .
14. 如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若 是“好玩三角形”,且 ,则 .15. 如图,有一条折线 ,它是由过 , , 组成的折线依次平移8,16,24,…个单位得到的,直线 与此折线有 ( 且为整数)个交点,则 的值为 .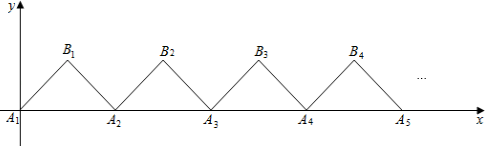 16. 如图,在圆心角为90°的扇形 中, , 为 上任意一点,过点 作 于点 ,设 为 的内心,当点 从点 运动到点 时,则内心 所经过的路径长为 .
16. 如图,在圆心角为90°的扇形 中, , 为 上任意一点,过点 作 于点 ,设 为 的内心,当点 从点 运动到点 时,则内心 所经过的路径长为 .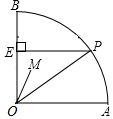
三、解答题
-
17.(1)、先化简: ,再从 的整数中选取一个你喜欢的 的值代入求值.(2)、解不等式组 ,并写出该不等式组的非负整数解.18. 某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
 (1)、本次共调查了名家长,扇形统计图中“很赞同”所对应的圆心角度数是度,并补全条形统计图 .(2)、该校共有3600名家长,通过计算估计其中“不赞同”的家长有多少名?(3)、从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.19. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温 (℃)与开机后用时 ( )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温 (℃)与时间 ( )的关系如图所示:
(1)、本次共调查了名家长,扇形统计图中“很赞同”所对应的圆心角度数是度,并补全条形统计图 .(2)、该校共有3600名家长,通过计算估计其中“不赞同”的家长有多少名?(3)、从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.19. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温 (℃)与开机后用时 ( )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温 (℃)与时间 ( )的关系如图所示: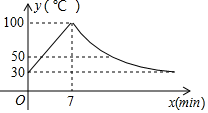 (1)、分别写出水温上升和下降阶段 与 之间的函数关系式;(2)、怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?20. 某校组织学生到恩格贝 和康镇 进行研学活动,澄澄老师在网上查得, 和 分
(1)、分别写出水温上升和下降阶段 与 之间的函数关系式;(2)、怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?20. 某校组织学生到恩格贝 和康镇 进行研学活动,澄澄老师在网上查得, 和 分别位于学校 的正北和正东方向, 位于 南偏东37°方向,校车从 出发,沿正北方向前往 地,行驶到15千米的 处时,导航显示,在 处北偏东45°方向有一服务区 ,且 位于 , 两地中点处.
 (1)、求 , 两地之间的距离;(2)、校车从 地匀速行驶1小时40分钟到达 地,若这段路程限速100千米/时,计算校车是否超速?
(1)、求 , 两地之间的距离;(2)、校车从 地匀速行驶1小时40分钟到达 地,若这段路程限速100千米/时,计算校车是否超速?(参考数据: , , )
21. 如图, 是⊙ 的直径,弦 ,垂足为 ,连接 .过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 .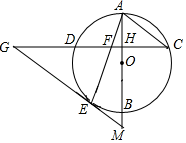 (1)、求证: 是⊙ 的切线;(2)、延长 交 的延长线于点 ,若 , ,求 的长.22. 某工厂制作 两种手工艺品, 每天每件获利比 多105元,获利30元的 与获利240元的 数量相等.(1)、制作一件 和一件 分别获利多少元?(2)、工厂安排65人制作 , 两种手工艺品,每人每天制作2件 或1件 .现在在不增加工人的情况下,增加制作 .已知每人每天可制作1件 (每人每天只能制作一种手工艺品),要求每天制作 , 两种手工艺品的数量相等.设每天安排 人制作 , 人制作 ,写出 与 之间的函数关系式.(3)、在(1)(2)的条件下,每天制作 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知 每件获利30元,求每天制作三种手工艺品可获得的总利润 (元)的最大值及相应 的值.23. 如图
(1)、求证: 是⊙ 的切线;(2)、延长 交 的延长线于点 ,若 , ,求 的长.22. 某工厂制作 两种手工艺品, 每天每件获利比 多105元,获利30元的 与获利240元的 数量相等.(1)、制作一件 和一件 分别获利多少元?(2)、工厂安排65人制作 , 两种手工艺品,每人每天制作2件 或1件 .现在在不增加工人的情况下,增加制作 .已知每人每天可制作1件 (每人每天只能制作一种手工艺品),要求每天制作 , 两种手工艺品的数量相等.设每天安排 人制作 , 人制作 ,写出 与 之间的函数关系式.(3)、在(1)(2)的条件下,每天制作 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知 每件获利30元,求每天制作三种手工艺品可获得的总利润 (元)的最大值及相应 的值.23. 如图 (1)、(探究发现)
(1)、(探究发现)如图1, 的顶点 在正方形 两条对角线的交点处, ,将 绕点 旋转,旋转过程中, 的两边分别与正方形 的边 和 交于点 和点 (点 与点 , 不重合).则 之间满足的数量关系是 .
(2)、(类比应用)如图2,若将(1)中的“正方形 ”改为“ 的菱形 ”,其他条件不变,当 时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)、(拓展延伸)如图3, , , , 平分 , ,且 ,点 是 上一点, ,求 的长.