吉林省2019年中考数学试卷
试卷更新日期:2019-08-06 类型:中考真卷
一、单选题
-
1. 如图,数轴上蝴蝶所在点表示的数可能为( )
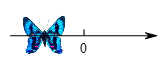 A、3 B、2 C、1 D、-12. 如图,由6个相同的小正方体组合成一个立体图形,它的俯视图为( )
A、3 B、2 C、1 D、-12. 如图,由6个相同的小正方体组合成一个立体图形,它的俯视图为( )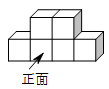 A、
A、 B、
B、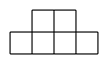 C、
C、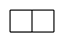 D、
D、 3. 若 为实数,则下列各式的运算结果比 小的是( )A、 B、 C、a×1 D、4. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
3. 若 为实数,则下列各式的运算结果比 小的是( )A、 B、 C、a×1 D、4. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( ) A、30° B、90° C、120° D、180°5. 如图,在 中, 所对的圆周角 ,若 为 上一点, ,则 的度数为( )
A、30° B、90° C、120° D、180°5. 如图,在 中, 所对的圆周角 ,若 为 上一点, ,则 的度数为( )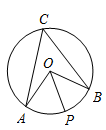 A、30° B、45° C、55° D、60°6. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
A、30° B、45° C、55° D、60°6. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( ) A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线
A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线二、填空题
-
7. 分解因式: =.
8. 不等式 的解集是 .9. 计算: .10. 若关于 的一元二次方程 有实数根,则 的值可以为(写出一个即可).11. 如图, 为 边 延长线上一点,过点 作 .若 , ,则 °.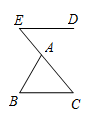 12. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .
12. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .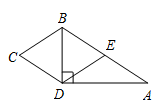 13. 在某一时刻,测得一根高为 的竹竿的影长为 ,同时同地测得一栋楼的影长为 ,则这栋楼的高度为 .14. 如图,在扇形 中, , 分别是半径 上的点,以 为邻边的 的顶点 在 上,若 ,则阴影部分图形的面积是(结果保留 ).
13. 在某一时刻,测得一根高为 的竹竿的影长为 ,同时同地测得一栋楼的影长为 ,则这栋楼的高度为 .14. 如图,在扇形 中, , 分别是半径 上的点,以 为邻边的 的顶点 在 上,若 ,则阴影部分图形的面积是(结果保留 ).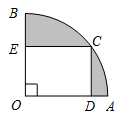
三、解答题
-
15. 先化简,再求值: ,其中 .16. 甲口袋中装有红色、绿色两把扇子,这两把扇子除颜色外无其他差别;乙口袋中装有红色、绿色两条手绢,这两条手绢除颜色外无其他差别.从甲口袋中随机取出一把扇子,从乙口袋中随机取出一条手绢,用画树状图或列表的方法,求取出的扇子和手绢都是红色的概率.
 17. 已知 是 的反比例函数,并且当 时, .(1)、求 关于 的函数解析式;(2)、当 时,求 的值.18. 如图,在 中,点 在边 上,以 为圆心, 长为半径画弧,交边 于点 ,连接 、 .求证: .
17. 已知 是 的反比例函数,并且当 时, .(1)、求 关于 的函数解析式;(2)、当 时,求 的值.18. 如图,在 中,点 在边 上,以 为圆心, 长为半径画弧,交边 于点 ,连接 、 .求证: .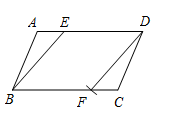 19. 图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 均为格点,按下列要求画图:
19. 图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 均为格点,按下列要求画图: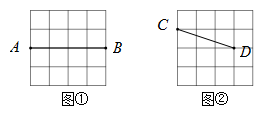 (1)、在图①中,以 为对角线画一个菱形 ,且 为格点;(2)、在图②中,以 为对角线画一个对边不相等的四边形 ,且 为格点, .20. 问题解决(1)、糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个?
(1)、在图①中,以 为对角线画一个菱形 ,且 为格点;(2)、在图②中,以 为对角线画一个对边不相等的四边形 ,且 为格点, .20. 问题解决(1)、糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个? (2)、反思归纳
(2)、反思归纳现有 根竹签, 个山楂.若每根竹签串 个山楂,还剩余 个山楂,则下列等式成立的是(填写序号).
⑴ ;⑵ ;⑶ .
21. 墙壁及淋浴花洒截面如图所示,已知花洒底座 与地面的距离 为 ,花洒 的长为 ,与墙壁的夹角 为43°.求花洒顶端 到地面的距离 (结果精确到 )(参考数据: , , )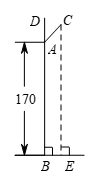 22. 某地区有城区居民和农村居民共80万人,某机构准备采用抽取样本的方法调查该地区居民“获取信息的最主要途径”.
22. 某地区有城区居民和农村居民共80万人,某机构准备采用抽取样本的方法调查该地区居民“获取信息的最主要途径”.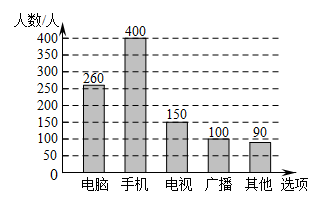 (1)、该机构设计了以下三种调查方案:
(1)、该机构设计了以下三种调查方案:方案一:随机抽取部分城区居民进行调查;
方案二:随机抽取部分农村居民进行调查;
方案三:随机抽取部分城区居民和部分农村居民进行调查.
其中最具有代表性的一个方案是;
(2)、该机构采用了最具有代表性的调查方案进行调查.供选择的选项有:电脑、手机、电视、广播,其他,共五个选项,每位被调查居民只选择一个选项.现根据调查结果绘制如下统计图,请根据统计图回答下列问题:①这次接受调查的居民人数为人;
②统计图中人数最多的选项为;
③请你估计该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的总人数 .
23. 甲、乙两车分别从 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到 地,乙车立即以原速原路返回到 地,甲、乙两车距 地的路程 与各自行驶的时间 之间的关系如图所示. (1)、m= , n=;(2)、求乙车距 地的路程 关于 的函数解析式,并写出自变量 的取值范围;(3)、当甲车到达 地时,求乙车距 地的路程24. 性质探究(1)、如图①,在等腰三角形 中, ,则底边 与腰 的长度之比为 .
(1)、m= , n=;(2)、求乙车距 地的路程 关于 的函数解析式,并写出自变量 的取值范围;(3)、当甲车到达 地时,求乙车距 地的路程24. 性质探究(1)、如图①,在等腰三角形 中, ,则底边 与腰 的长度之比为 .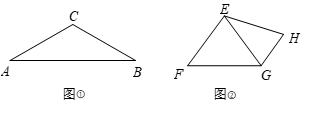 (2)、理解运用
(2)、理解运用若顶角为120°的等腰三角形的周长为 ,则它的面积为;
(3)、如图②,在四边形 中, .①求证: ;
②在边 上分别取中点 ,连接 .若 , ,直接写出线段 的长.
(4)、类比拓展顶角为 的等腰三角形的底边与一腰的长度之比为(用含 的式子表示).
25. 如图,在矩形 中, , 为边 上一点, ,连接 .动点 从点 同时出发,点 以 的速度沿 向终点 运动;点 以 的速度沿折线 向终点 运动.设点 运动的时间为 ,在运动过程中,点 ,点 经过的路线与线段 围成的图形面积为 .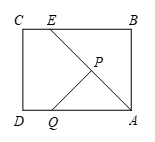
 (1)、 , °;(2)、求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当 时,直接写出 的值.26. 如图,抛物线 与x轴相交于 两点(点 在点 的左侧),与 轴相交于点 . 为抛物线上一点,横坐标为 ,且 .
(1)、 , °;(2)、求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当 时,直接写出 的值.26. 如图,抛物线 与x轴相交于 两点(点 在点 的左侧),与 轴相交于点 . 为抛物线上一点,横坐标为 ,且 .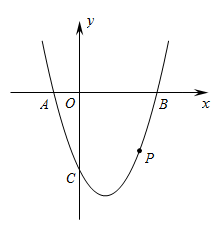 (1)、求此抛物线的解析式;(2)、当点 位于 轴下方时,求 面积的最大值;(3)、设此抛物线在点 与点 之间部分(含点 和点 )最高点与最低点的纵坐标之差为 .
(1)、求此抛物线的解析式;(2)、当点 位于 轴下方时,求 面积的最大值;(3)、设此抛物线在点 与点 之间部分(含点 和点 )最高点与最低点的纵坐标之差为 .①求 关于 的函数解析式,并写出自变量 的取值范围;
②当 时,直接写出 的面积.