浙江省湖州市长兴县2018-2019学年七年级下学期数学第三次月考试卷

试卷更新日期：2019-08-05 类型：月考试卷

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 若分式 $\frac{x - 2}{x + 5}$ 的值为0，则 $x$ 的值是（）

A、2 B、0 C、-2 D、-5

查看试题解析
2. 下列各式中是二元一次方程的是（）

A、x-3y=5 B、xy-y=1 C、2x+3y D、 $\frac{x}{2}$ + $\frac{7}{y}$ = $\frac{1}{5}$

查看试题解析
3. 如图，图①，图②，图③，图④这四个图形中，可以由图A平移得到的是（）

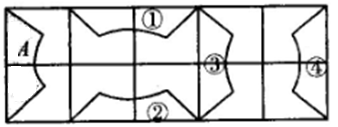A、图① B、图② C、图③ D、图④

查看试题解析
4. 下列多项式能用公式法分解因式的是（）

A、4x²+(-y)² B、-4x²-y² C、x+1+ $\frac{x^{2}}{4}$ D、x²+2xy-y²

查看试题解析
5. 如图，已知∠1=∠2，则能得到正确的结论是（）

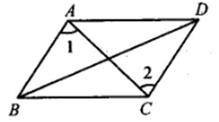A、AC⊥AB B、AB=CD C、AD∥BC D、AB∥CD

查看试题解析
6. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简过程如图所示：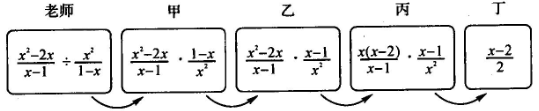

接力中，自己负责的一步出现错误的是（）

A、只有乙 B、乙和丁 C、乙和丙 D、甲和丁

查看试题解析
7. 若x+y=3且xy=1，则代数式(1+x)(1+y)的值是（）

A、-1 B、1 C、3 D、5

查看试题解析
8. 学校为创建“书香校园”，购买了一批图书．已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本．求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元，则可列方程为（）

A、 $\frac{10000}{x} - \frac{9000}{x - 5} = 100$ B、 $\frac{9000}{x - 5} - \frac{10000}{x} = 100$ C、 $\frac{10000}{x - 5} - \frac{9000}{x} = 100$ D、 $\frac{9000}{x} - \frac{10000}{x - 5} = 100$

查看试题解析
9. 若(a+b)⁹=-1，(a-b)¹⁰=1，则a¹⁹+b¹⁹的值是（）

A、2 B、0 C、-1 D、0或-1

查看试题解析
10. 请你估计一下 $\frac{(2^{2} - 1) (3^{2} - 1) (4^{2} - 1) .... (2018^{2} - 1) (2019^{2} - 1)}{1^{2} \cdot 2^{2} \cdot 3^{2} {....2018}^{2} \cdot 2019^{2}}$ 的值应该最接近于（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{2018}$ D、 $\frac{1}{2019}$

查看试题解析

二、填空题(每小题2分，共12分)

11. 因式分解：5x²-2x= ．

查看试题解析
12. 如图，CD∥AB，点F在AB上，EF⊥GF，F为垂足，若∠1=48°，则∠2的度数为．

查看试题解析
13. 若（x+m）与（x+3）的乘积中不含x的一次项，则m的值为.

查看试题解析
14. 若关于x的方程 $\frac{2}{x - 2}$ + $\frac{x + m}{2 - x}$ =2有增根，则m的值是．

查看试题解析
15. 如图所示的两架天平保持平衡，且每块巧克力的质量相等，每个果冻的质量也相等，则一块巧克力的质量是克(g)．

查看试题解析
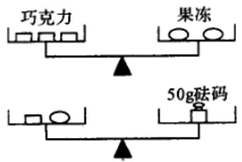16. 新定义一种运算：a@b=(a+b)²-(a-b)² ，下面给出关于这种运算的几个结论：①1@(-2)=-8；②a@b=b@a；③若a@b=0，则a一定为0；④若a+b=0，则(a@a)+(b@b)=8a² ．其中正确结论的序号是．

查看试题解析

三、解答题(共58分)

17. 计算：

(1)、2019⁰-( $\frac{1}{2}$ )^-1

(2)、 $\frac{2 a}{2 a - b} + \frac{b}{b - 2 a}$

查看试题解析
18. 解方程(组)：

(1)、 $\frac{x + 3}{2 x - 3} = \frac{2}{7}$

(2)、 ${\begin{cases} 2 x + 3 y = 44 \\ x + 4 y = 42 \end{cases}$

查看试题解析
19. 先化简再求值： $(\frac{3 x}{x - 2} - \frac{x}{x - 2}) \div \frac{x}{x^{2} - 4}$ ，其中x=-1

查看试题解析
20. 如图，已知BD∥CE，AC⊥BD于点G．

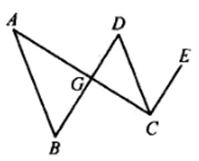(1)、求∠ACE的度数；

(2)、若∠B=∠DCE，请问AB与CD是否平行？并说明理由．

查看试题解析
21. 两位同学将一个二次三项式分解因式，一位同学因看错了一次项系数而分解成3(x-1)(x-9)，另一位同学因看错了常数项而分解成3(x-2)(x-4)

(1)、求原来的二次三项式；

(2)、将(1)中的二次三项式分解因式

查看试题解析
22. 甲、乙两地间的铁路运行路程为1400千米，列车将原来运行的平均速度提高 $\frac{1}{3}$ 后，运行的时间减少 $\frac{5}{3}$ 小时，求列车原来运行的平均速度．

查看试题解析
23. 如图，已知AM∥BN，∠B=40°，点P是射线BN上一动点(与点B不重合)，AC，AD分别平分∠BAP和∠PAM，交射线BN于点C，D．

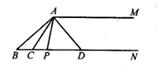(1)、求∠CAD的度数；

(2)、当点P运动时，∠APB与∠ADB之间存在怎样的数量关系？说明理由；

(3)、当点P运动到使∠ACB=∠BAD时，求∠BAC的度数

查看试题解析
24. 某校举办“迎冬奥会“学生书画展览，现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品．

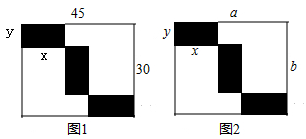(1)、如图1，若大长方形的长和宽分别为45米和30米，设小长方形的长为x，宽为y，求出x和y的值．

(2)、如图2，若大长方形的长和宽分别为a和b．
①求出1个小长方形周长与大长方形周长之比；

②若作品展览区域(阴影部分)面积占展厅面积的 $\frac{1}{3}$ ，求x和y的数量关系．

查看试题解析