浙江省湖州市长兴县2018-2019学年九年级下学期数学第三次月考试卷
试卷更新日期:2019-08-05 类型:月考试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
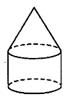
1. 计算-2+1的正确结果是( )A、-2 B、-3 C、1 D、-12. 若二次根式 有意义,则x的取值范围是( )A、x> B、x≥ C、x≤ D、x≤53. 一个由圆柱和圆锥组成的几何体如右图水平放置,其主视图为( )
 A、
A、 B、
B、 C、
C、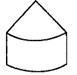 D、
D、 4. 小时候我们用肥皂水吹泡泡,其泡沫的厚度是约0.000326毫米,数字0.000326用科学记数法表示为( )A、3.26×10-4 B、0.326×10-3 C、3.26×104 D、32.6×10-55. 学校组织的爱心经贸节有一个摊位游戏,是先旋转一个转盘的指针,如果指针箭头停在奇数的位置,玩的人就可以从袋子抽出一个弹珠转盘和袋子里的弹珠如图所示,当抽到黑色的弹珠就能得到奖品,小丽玩了这个游戏,则小丽得到奖品的可能性为( )
4. 小时候我们用肥皂水吹泡泡,其泡沫的厚度是约0.000326毫米,数字0.000326用科学记数法表示为( )A、3.26×10-4 B、0.326×10-3 C、3.26×104 D、32.6×10-55. 学校组织的爱心经贸节有一个摊位游戏,是先旋转一个转盘的指针,如果指针箭头停在奇数的位置,玩的人就可以从袋子抽出一个弹珠转盘和袋子里的弹珠如图所示,当抽到黑色的弹珠就能得到奖品,小丽玩了这个游戏,则小丽得到奖品的可能性为( ) A、不可能 B、非常有可能 C、不太可能 D、一定能6. 如图,对三角形中的尺规作图描述正确的是( )
A、不可能 B、非常有可能 C、不太可能 D、一定能6. 如图,对三角形中的尺规作图描述正确的是( )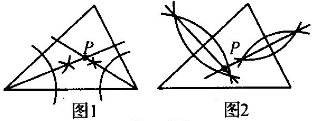 A、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的重心 B、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的外心 C、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的内心 D、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的重心7. 某次知识竞赛共有25道题,规定:每答对一道得+4,每答错一题得-2分,不答的题得0分,已知王婷这次竞赛得了76分,设王婷答对了x道题,答错了y道题,则x,y满足的方程是( )A、x-y=25 B、x+y=25 C、4x-2y=76 D、4x+2y=768. 如图,已知AB是⊙O的直径,若∠BAC=60°,AC=3,则 的长为( )
A、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的重心 B、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的外心 C、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的内心 D、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的重心7. 某次知识竞赛共有25道题,规定:每答对一道得+4,每答错一题得-2分,不答的题得0分,已知王婷这次竞赛得了76分,设王婷答对了x道题,答错了y道题,则x,y满足的方程是( )A、x-y=25 B、x+y=25 C、4x-2y=76 D、4x+2y=768. 如图,已知AB是⊙O的直径,若∠BAC=60°,AC=3,则 的长为( )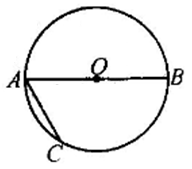 A、4π B、2π C、 π D、π9. 如图,将菱形纸片ABCD折叠使点A恰好落在菱形的对称中心O处,折痕为EF,再次折叠图形,使点C恰好落在EF的中点G处,折痕为MN.若菱形ABCD的边长为2,∠A=120°,则MN的长度为( )
A、4π B、2π C、 π D、π9. 如图,将菱形纸片ABCD折叠使点A恰好落在菱形的对称中心O处,折痕为EF,再次折叠图形,使点C恰好落在EF的中点G处,折痕为MN.若菱形ABCD的边长为2,∠A=120°,则MN的长度为( ) A、 B、2 C、 D、10. 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点C是第四象限内抛物线上一点,连结AC,BC.下列所给条件中,能确定二次项系数a的值的是( )
A、 B、2 C、 D、10. 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点C是第四象限内抛物线上一点,连结AC,BC.下列所给条件中,能确定二次项系数a的值的是( ) A、A(2,0),B(6,0),AC=BC B、AB=2,C(3,-1) C、∠ACB=90°,点C的纵坐标为-2 D、A(2,0),AB=2AC
A、A(2,0),B(6,0),AC=BC B、AB=2,C(3,-1) C、∠ACB=90°,点C的纵坐标为-2 D、A(2,0),AB=2AC二、填空题(本题有6小题,每小题4分,共24分)
-
11. 分解因式:3-3a2 。12. 某校九年级在“唱响《我和我的祖国》”比赛中,各班代表队得分如下(单位:分):8,7,9,6,9,7,8,则各代表队得分的中位数是。13. 在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴对称点C的坐标为。14. 如图,是小明荡秋千的侧面示意图,秋千链长AB=5m(秋千踏板视作一个点),静止时秋千位于铅垂线BC上,此时秋千踏板A到地面的距离为0.5m.当秋千踏板摆动到点D时,点D到BC的距离DE=4m.若他从D处摆动到D'处时,恰好D'B⊥DB,则D'到地面的距离为 m.
 15. 已知:当n≤x≤n+1时,二次函数y=x2-3x+3的最小值为1,则n的值为。16. 如图,已知△ABC,AC=2AB,延长AB至点D,使得BD=AB,连结CD,若CD与△ABC的外接圆⊙O相切,则cos∠OAC=。
15. 已知:当n≤x≤n+1时,二次函数y=x2-3x+3的最小值为1,则n的值为。16. 如图,已知△ABC,AC=2AB,延长AB至点D,使得BD=AB,连结CD,若CD与△ABC的外接圆⊙O相切,则cos∠OAC=。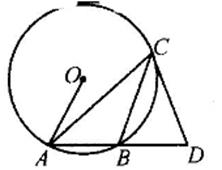
三、|解答题(本题有8小题,共66分)
-
17. 计算:(-2)2×|-2|-( )018. 先化简,再求值 ,其中x= -1.19. 如图,已知等腰△ABC中,AB=AC,点D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF。
 20. 某校准备在七年级成立“民族乐器”、“经典诵读“、”传统礼仪”和“地方戏曲”等四个课外活动小组.现随机调查40名学生的报名意向(每人最多选择一个小组),并绘制如下两幅不完整的统计图:
20. 某校准备在七年级成立“民族乐器”、“经典诵读“、”传统礼仪”和“地方戏曲”等四个课外活动小组.现随机调查40名学生的报名意向(每人最多选择一个小组),并绘制如下两幅不完整的统计图: (1)、本次随机调查的学生中,不参加课外活动小组的有多少人?并将条形图补充完整;(2)、已知该校七年级共有400名学生,请估计参加课外活动小组的学生有多少人?21. 某农夫将苹果树种在正方形的果园里为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.如图,我们可以看到农夫所种植苹果树的列数n和苹果树数量及针叶树数量的规律:
(1)、本次随机调查的学生中,不参加课外活动小组的有多少人?并将条形图补充完整;(2)、已知该校七年级共有400名学生,请估计参加课外活动小组的学生有多少人?21. 某农夫将苹果树种在正方形的果园里为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.如图,我们可以看到农夫所种植苹果树的列数n和苹果树数量及针叶树数量的规律: (1)、完成下表中的空格:
(1)、完成下表中的空格:列数
苹果树数y1
针叶树数y2
1
1
8
2
4
3
9
24
4
16
32
5
(2)、分别写出y1 , y2关于n的函数关系式;(3)、若农夫想要种更多列,做一个更大的果园,当农夫将果园扩大时,哪种树的需求量更大?22. 如图,在 ABCD中,E为对角线AC上一点,以CD,CE为边作 CDFE,边EF与AD交于点G,连结AF,BE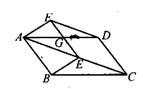 (1)、求证:△AFD≌△BEC;(2)、若∠AFD-∠EAB=90°,AF=3,sin∠BAE= ,
(1)、求证:△AFD≌△BEC;(2)、若∠AFD-∠EAB=90°,AF=3,sin∠BAE= ,①求AE的长;
②当BC的长为何值时, CDFE为菱形?并说明理由。
23. 某通讯经营店销售A,B两种品牌儿童手机,今年的进货和销售价格如表:A型手机
B型手机
进货价格(元/只)
1000
1100
销售价格(元/只)
x
1500
已知A型手机去年1月份销售总额为4万元,今年经过改造升级后每只销售价比去年增加200元.今年1月份A型手机的销售数量与去年1月份相同,而销售总额比去年1月份增加20%.
(1)、今年1月份A型手机的销售价是多少元?(2)、该店计划6月份再进一批A型和B型手机共50只且B型手机数量不超过A型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?(3)、该店为吸引客源,准备增购一种进价为500元的C型手机,预算用8万元购进这三种手机若干只,其中A型与B型的数量之比为1:2,则该店至少可以购进三种手机共多少只?24. 如图,在平面直角坐标系xOy中,已知矩形OABC的边OA,OC都在坐标轴上,点B的坐标为(12,16).点D以每秒5个单位的速度从点C向点A运动(不与A,C重合),反比例函数y= (x>0)的图象经过点D,与AC的另一个交点为E,与AB,BC分别交于点FG,连结EF.设点D的运动时间为t.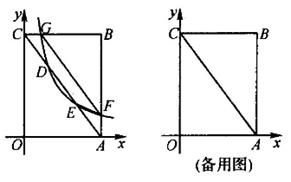 (1)、当t=1时,求反比例函数y= (x>0)的解析式;(2)、点D在运动过程中,
(1)、当t=1时,求反比例函数y= (x>0)的解析式;(2)、点D在运动过程中,①求证:当线段AF的长度取最大值时,点D恰好为AC的中点;
②是否存在这样的t,使得△AEF为等腰三角形?若存在,请求出此时点D的坐标;若不存在,请说明理由;
(3)、连结FG,将△BFG沿着FG所在直线翻折,当点B落在y轴左侧时,请直接写出t的取值范围.