浙江省杭州市四校2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2019-08-05 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列选项中，具有相反意义的量是 $($ $)$

A、盈利3万元与支出3万元 B、气温升高 $3 ℃$ 与气温为 $- 3 ℃$ C、胜二局与负三局 D、甲乙两队篮球比赛比分分别为65：60与60：65

查看试题解析
2. 在 $\frac{1}{7} ， - π ， 0.314 ， - \sqrt{2} ， 0.3 ， - \sqrt{49} ， 3 \frac{1}{3}$ 中无理数有 $($ $)$ 个.

A、1 B、2 C、3 D、4

查看试题解析
3. 下列运算中正确的是 $($ $)$

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $- 2^{4} \times \frac{1}{8} = 2$ C、 ${(- 2)}^{2} \times {(- 3)}^{2} = 36$ D、 $\sqrt{16} = \pm 4$

查看试题解析
4. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划“一带一路”地区覆盖总人口44亿，这个数用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁹ C、4.4×10⁸ D、4.4×10¹⁰

查看试题解析
5. 若 ${(a - 2)}^{2} + | b + 3 | = 0$ ，则 ${(a + b)}^{2017}$ 的值是（）

A、 $0$ B、 $1$ C、 $- 1$ D、 $- 2017$

查看试题解析
6. 下列说法： $①$ 两个无理数的和可能是有理数； $②$ 任意一个有理数都可以用数轴上的点表示； $③ - πmn + 3^{3}$ 是三次二项式； $④$ 立方根是本身的数有0和1； $⑤$ 小明的身高约为 $1.7$ 米，则他身高的准确值a的范围是 $1.65 \leq a \leq 1.74.$ 其中正确的有 $($ $)$ 个

A、1 B、2 C、3 D、4

查看试题解析
7. 若单项式 $7 x^{2 n} y^{m - n}$ 与单项式 $- 3 x^{6} y^{2 n}$ 的和是 $4 x^{2 n} y^{2 n}$ ，则m与n的值分别是 $($ $)$

A、 $m = 3$ ， $n = 9$ B、 $m = 9$ ， $n = 9$ C、 $m = 9$ ， $n = 3$ D、 $m = 3$ ， $n = 3$

查看试题解析
8. 计算： $| 1 - \sqrt{5} | + | 3 - \sqrt{5} | - | 3.14 - π | =$ （）

A、 $0.86 - 2 \sqrt{5} + π$ B、 $5.14 - π$ C、 $2 \sqrt{5} - 7.14 + π$ D、 $- 1.14 + π$

查看试题解析
9. 下列各式： $① - a$ ； $② - | x |$ ； $③ - a^{2}$ ； $④ - a^{2} - 1$ ； $⑤ a^{2} - {(a + 1)}^{2}$ ，其中值一定是负数的有 $($ $)$ 个.

A、1 B、2 C、3 D、4

查看试题解析
10. 电子跳蚤游戏盘 $($ 如图 $)$ 为 $△ ABC$ ， $AB = 7$ ， $AC = 8$ ， $BC = 9$ ，如果电子跳蚤开始时在BC边的 $P_{0}$ 点， ${BP}_{0} = 3$ ，第一步跳蚤从 $P_{0}$ 跳到AC边上 $P_{1}$ 点，且 ${CP}_{1} = {CP}_{0}$ ；第二步跳蚤从 $P_{1}$ 跳到AB边上 $P_{2}$ 点，且 ${AP}_{2} = {AP}_{1}$ ；第三步跳蚤从 $P_{2}$ 跳回到BC边上 $P_{3}$ 点，且 ${BP}_{3} = {BP}_{2}$ ； $\dots$ 跳蚤按上述规则跳下去，第n次落点为 $P_{n}$ ，则 $P_{5}$ 与 $P_{2018}$ 之间的距离为 $($ $)$

A、0 B、2 C、4 D、5

查看试题解析

二、填空题

11. 64的算术平方根是.

查看试题解析
12. 大于 $- π$ 且小于 $- \sqrt{2}$ 的所有整数的和是.

查看试题解析
13. 已知 $x^{2} = 2 y - 2$ ，则代数式 $6 - 3 x^{2} + 6 y$ 的值为.

查看试题解析
14. 在下列式子中： $\frac{b^{2}}{3}$ ， $\frac{xy}{2} + 3$ ，2， $\frac{3}{xy}$ ， $\frac{ab + x}{5}$ ， $\frac{a + b}{π}$ ， $\frac{(2 + π) xy}{3}$ ，多项式有个 $.$

查看试题解析
15. 已知 $| a - 1 | = 3$ ， $| b | = 3$ ，a，b在数轴上对应的点分别为A、B，则A，B两点间距离等于.

查看试题解析
16. 已知当 $x = 5$ 时， ${ax}^{15} + {bx}^{13} + {cx}^{11} + 5 = 9$ ，则 $x = - 5$ 时， ${ax}^{15} + {bx}^{13} + {cx}^{11} + 5$ 的值为.

查看试题解析
17. 若实数a，b，c满足关系式 $\sqrt{a - 9 + b} + \sqrt{9 - a - b} = \sqrt{4 a - c + 4 b}$ ，则c的平方根为.

查看试题解析
18. 如图1，将一个边长为 $a$ 的正方形纸片剪去两个小矩形，得到一个“ ”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长为.

查看试题解析

三、解答题

19. 计算

(1)、 $(- \frac{3}{7}) \times 21 \times \sqrt{2} ($ 保留一位小数， $\sqrt{2} \approx 1.41)$

(2)、 $- 2^{4} - 24 \times (\frac{1}{3} - \frac{5}{6} + \frac{3}{4})$

查看试题解析
20. 化简求值：已知整式 $2 x^{2} + ax - y + 6$ 与整式 $2 {bx}^{2} - 3 x + 5 y - 1$ 的差不含x和 $x^{2}$ 项，试求 $4 (a^{2} + 2 b^{3} - a^{2} b) + 3 a^{2} - 2 (4 b^{3} + 2 a^{2} b)$ 的值.

查看试题解析
21. 将下列各数表示在数轴上，并将它们按从小到大的顺序排列，用“ $<$ ”连接. $① - 3$ 的相反数； $② - 27$ 的立方根； $③ \sqrt{6}$ 的平方根； $④ - 2$ 的倒数.

查看试题解析
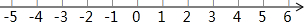22. 把下列各数的序号填在相应的大括号内：
①﹣17；②π；③﹣|﹣ $\frac{8}{5}$ |；④ $\sqrt{3} - 1$ ；⑤ $\sqrt{\frac{1}{36}}$ ；⑥﹣0.92；⑦ $- 2 + \sqrt{3}$ ；⑧﹣0. $\overset{\cdot}{5}$ ；⑨1.2020020002；

(1)、正实数{           }
负有理数{          }

无理数{          }

(2)、从以上9个数中选取2个有理数，2个无理数，用“+、﹣、×、÷”中的3种不同的运算符号将选出的4个数进行运算（可以用括号），使得计算结果为正整数，列出式子并计算.

查看试题解析
23. 某商场将进货价为35元台灯以50元销售价售出，平均每月能售出500个，市场调研表明：当销售价每上涨1元时，其销售量就将减少10个 $.$ 若设每个台灯的销售价上涨a元.

(1)、试用含a的代数式填空：涨价后，每个台灯的销售价为元，利润为元，商场的台灯平均每月的销售量为台 $.$

(2)、如果商场要想销售利润平均每月达到10000，商场经理甲说：“在原售价每台50元的基础上再上涨25元，可以完成任务”，商场经理乙说：“不用涨那么多，在原售价每台50元的基础上再上涨15元就可以了”，为减少库存，应该采取谁的意见？

查看试题解析
24. （阅读理解）如果点M，N在数轴上分别表示实数m，n，在数轴上M，N两点之间的距离表示为 $MN = m - n (m > n)$ 或 $MN = n - m (n > m)$ 或 $| m - n |$ .
利用数形结合思想解决下列问题：已知数轴上点A与点B的距离为12个单位长度，点A在原点的左侧，到原点的距离为24个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒2个单位的速度向终点C移动，设移动时间为t秒.

(1)、点A表示的数为，点B表示的数为.

(2)、用含t的代数式表示P到点A和点C的距离： $PA =$ ， $PC =$ .

(3)、当点P运动到B点时，点Q从A点出发，以每秒4个单位的速度向C点运动，Q点到达C点后，立即以同样的速度返回，运动到终点A，在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由.

查看试题解析