浙江省绍兴市嵊州市2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 9的相反数是( )A、 ﹣9 B、9 C、 D、2. 嵊州新城吾悦广场,总建筑面积58万平方米,西临剡溪大桥,南接环城南路,东为高丰路,北临剡溪,占据城南新区核心地段,已成为嵊州城市新中心,将数58万用科学记数法表示为A、 B、 C、 D、3. 把一根木条固定在墙面上,至少需要两枚钉子,这样做的数学依据是( )A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、两点之间直线最短4. 将方程 去分母得( )A、 B、 C、 D、5. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( )
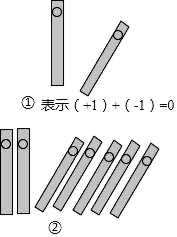 A、﹣1 B、﹣2 C、﹣3 D、﹣46. 下列各题中的两项是同类项的是( )A、 和- ; B、 和 ; C、 和9bc; D、 和 .7. 将四个数 , , , 表示在数轴上,被如图所示的墨迹覆盖的数是(
A、﹣1 B、﹣2 C、﹣3 D、﹣46. 下列各题中的两项是同类项的是( )A、 和- ; B、 和 ; C、 和9bc; D、 和 .7. 将四个数 , , , 表示在数轴上,被如图所示的墨迹覆盖的数是( A、 B、 C、 D、8. 某款服装进价120元 件,标价x元 件,商店对这款服装推出“买两件,第一件原价,第二件打六折”的促销活动,按促销方式销售两件该款服装,商店仍获利48元,则x的值为A、185 B、190 C、180 D、1959. 若 时, 式子的值为2033,则当 时,式子 的值为A、2018 B、2019 C、 D、10. 如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到A1 , 第2次移动到A2 , 第3次移动到A3 , ……,第n次移动到An , 则△OA2A2019的面积是( )
A、 B、 C、 D、8. 某款服装进价120元 件,标价x元 件,商店对这款服装推出“买两件,第一件原价,第二件打六折”的促销活动,按促销方式销售两件该款服装,商店仍获利48元,则x的值为A、185 B、190 C、180 D、1959. 若 时, 式子的值为2033,则当 时,式子 的值为A、2018 B、2019 C、 D、10. 如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到A1 , 第2次移动到A2 , 第3次移动到A3 , ……,第n次移动到An , 则△OA2A2019的面积是( )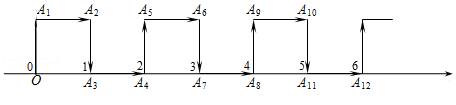 A、504 B、 C、 D、1009
A、504 B、 C、 D、1009二、填空题
-
11. 计算: .12. “x的2倍与1的差”用代数式可表示为.13. 9的算术平方根是 , = , ﹣ = .14. 在实数:1, , , , , 两个1之间一次多一个 中,无理数有个15. 钟表上的时间指示为两点半,此时时针与分针所成的角 小于平角 的度数为.16. 如图,已知点O在直线AB上, ,OD平分 , ,则 的度数为.
 17. 某校建立了一个身份识别系统,图1是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左往右依次记为a,b,c,d,那么可以转换为该生所在的班级序号,其序号为 ,如图1,第一行数字从左往右依次为0,1,0,1,序号为 ,表示该生为5班学生,则图2识别图案的学生所在班级为班
17. 某校建立了一个身份识别系统,图1是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左往右依次记为a,b,c,d,那么可以转换为该生所在的班级序号,其序号为 ,如图1,第一行数字从左往右依次为0,1,0,1,序号为 ,表示该生为5班学生,则图2识别图案的学生所在班级为班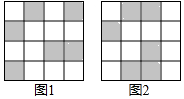 18. 如图,点A、B为数轴上的两点,O为原点,A、B表示的数分别是x、x+2,B、O两点之间的距离等于A、B两点间的距离,则x的值是.
18. 如图,点A、B为数轴上的两点,O为原点,A、B表示的数分别是x、x+2,B、O两点之间的距离等于A、B两点间的距离,则x的值是.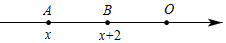 19. 按下面的程序计算:
19. 按下面的程序计算:
如果输入x的值是正整数,输出结果是150,那么满足条件的x的值有个
20. 父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米 小时,如果再载了另一个人,则速度为20千米 小时 摩托车不允许带两个人,即每车至多载两人 每个儿子如果步行速度为5千米 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为小时.21. 已知a、b、c为非零实数,请你探究以下问题:(1)、当 时, ;当 时, .(2)、若 那么 的值为.22. 如图1,OP为一条拉直的细线,长为7cm,A,B两点在OP上,若先握住点B,将OB折向BP,使得OB重叠在BP上,如图 再从图2的A点及与A点重叠处一起剪开,使得细线分成三段 若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为cm.
三、解答题
-
23. 先化简,再求值.
,其中 , .
24. 计算(1)、(2)、25. 解方程(1)、(2)、26. 有一个水库某天8:00的水位为 以警戒线为基准,记高于警戒线的水位为正 在以后的6个时刻测得的水位升降情况如下 记上升为正,单位: :, ,0, , ,
经过6次水位升降后,水库的水位超过警戒线了吗?
27. 如图, 方格中每个小正方形的边长都为1. (1)、直接写出图 中正方形ABCD的面积及边长;(2)、在图 的 方格中,画一个面积为8的格点正方形 四个顶点都在方格的顶点上 ;并把图 中的数轴补充完整,然后用圆规在数轴上表示实数 .28. 某校学生会主席换届选举,经初选、复选后,共有甲,乙,丙三人进入最后的竞选,最后决定用投票方式进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开票,结果如表所示: 单位:票
(1)、直接写出图 中正方形ABCD的面积及边长;(2)、在图 的 方格中,画一个面积为8的格点正方形 四个顶点都在方格的顶点上 ;并把图 中的数轴补充完整,然后用圆规在数轴上表示实数 .28. 某校学生会主席换届选举,经初选、复选后,共有甲,乙,丙三人进入最后的竞选,最后决定用投票方式进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开票,结果如表所示: 单位:票投票箱
候选人
废票
合计
甲
乙
丙
一
200
211
147
12
570
二
244
15
630
三
97
41
205
7
350
四
250
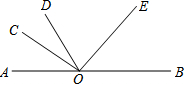
(1)、若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数.(2)、根据 题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程.29. 如果两个角的差的绝对值等于 ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如, , , ,则 和 互为反余角,其中 是 的反余角, 也是 的反余角.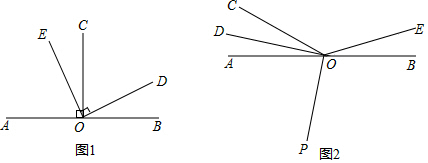 (1)、如图 为直线AB上一点, 于点O, 于点O,则 的反余角是 , 的反余角是;(2)、若一个角的反余角等于它的补角的 ,求这个角.(3)、如图2,O为直线AB上一点, ,将 绕着点O以每秒 角的速度逆时针旋转得 ,同时射线OP从射线OA的位置出发绕点O以每秒 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时, 与 互为反余角 图中所指的角均为小于平角的角 .30. 观察下列等式: , , ,则以上三个等式两边分别相加得: .
(1)、如图 为直线AB上一点, 于点O, 于点O,则 的反余角是 , 的反余角是;(2)、若一个角的反余角等于它的补角的 ,求这个角.(3)、如图2,O为直线AB上一点, ,将 绕着点O以每秒 角的速度逆时针旋转得 ,同时射线OP从射线OA的位置出发绕点O以每秒 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时, 与 互为反余角 图中所指的角均为小于平角的角 .30. 观察下列等式: , , ,则以上三个等式两边分别相加得: .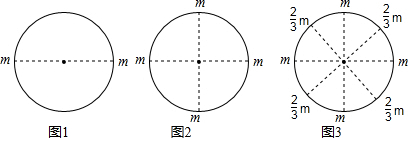 (1)、观察发现
(1)、观察发现; .
(2)、拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆 如图 ,在每个分点标上质数m,记2个数的和为 ;第二次再将两个半圆周都分成 圆周 如图 ,在新产生的分点标上相邻的已标的两数之和的 ,记4个数的和为 ;第三次将四个 圆周分成 圆周 如图 ,在新产生的分点标上相邻的已标的两数之和的 ,记8个数的和为 ;第四次将八个 圆周分成 圆周,在新产生的分点标上相邻的已标的两个数的和的 ,记16个数的和为 ; 如此进行了n次.
用含m、n的代数式表示 ;
当 时,求 的值.