浙江省宁波市镇海区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 2018的相反数是( )A、 ﹣2018 B、 C、2018 D、2. 下列各式中,是一元一次方程的是( )A、 B、 C、 D、3. 2018年全国高考报名总人数是975万人,用科学记数法表示为( )A、 人 B、 人 C、 人 D、 人4. 数轴上 、 两点表示的数分别是-3和3,则 ,-4, , 表示的点位于 、 两点之间的是( )A、 B、-4 C、 D、5. 宁波市2018年上半年地方财政收入约837.90亿元,这个数精确到( )A、百万位 B、百分位 C、千万位 D、十分位6. 下列各数中:0, , , , ,0.010010001是无理数的有( )A、1个 B、2个 C、3个 D、4个7. 若 ,则代数式 的值为( )A、-2 B、2 C、10 D、148. 规定新运算“ ”:对于任意实数 、 都有 ,例如: ,则 的解是( )A、-1 B、1 C、5 D、-59. 实数 , 在数轴上的位置如图所示,则下列结论正确的是( )
 A、 B、 C、 D、10. 如图,在长为 ,宽为 的长方形(其中 )中放置如图所示的两个相同的正方形,恰好构成三个形状、大小完全一样的小长方形(阴影部分),则放置的正方形的边长为( )
A、 B、 C、 D、10. 如图,在长为 ,宽为 的长方形(其中 )中放置如图所示的两个相同的正方形,恰好构成三个形状、大小完全一样的小长方形(阴影部分),则放置的正方形的边长为( )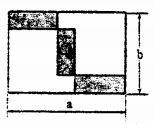 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 单项式 的系数是 , 次数是 , 多项式 的次数是.12. 若 与 是同类项,则 , ;合并以后的结果是.13. 如图所示,如果用20米长的铝合金做一个长方形的窗框,设长方形窗框的三根横条长均为 米,则长方形窗框的竖条长均为米(用含 的代数式表示).
 14. 某工程甲单独完成需4天,乙单独完成需8天,现甲先工作1天,乙再加入合作,问甲、乙再合作几天才能完成这项工程。设甲、乙再合作 天才能完成这项工程,则可列一元一次方程.15. 如图,线段 ,点 在直线 上, , 、 分别是线段 、 的中点,则 的长为.
14. 某工程甲单独完成需4天,乙单独完成需8天,现甲先工作1天,乙再加入合作,问甲、乙再合作几天才能完成这项工程。设甲、乙再合作 天才能完成这项工程,则可列一元一次方程.15. 如图,线段 ,点 在直线 上, , 、 分别是线段 、 的中点,则 的长为. 16. 按下面的程序计算,若开始输入的值 为正整数:
16. 按下面的程序计算,若开始输入的值 为正整数:
规定:程序运行到“判断结果是否大于10”为一次运算,当 时,输出结果=;若经过2次运算就停止,则 可以取的所有值是.
17. 设 , , , , , ,…, , , ,…, ,…,在这列数中,第50个数是.三、解答题
-
18. 计算:(1)、(2)、19. 先化简,再求值.求当 , 时,代数式 的值.20. 解方程.(1)、(2)、21. 如图所示,点 、 、 分别代表三个村庄,根据下列条件画图.

①画射线 ,画线段 ,画直线 ;
②若线段 是连结 村和 村的一条公路,现 村庄也要修一条公路与 、 两村庄之间的公路连通,为了使修建的路程最短, 村庄应该如何修路?请在同一图上用三角板画出示意图,并说明这样修路的理由.
22. 寒假将至,某班家委会组织学生到北京旅游,现联系了一家旅行社,这家旅行社报价为4000元/人,但根据具体报名情况推出了优惠举措:人数
10人及以下(含10人)
超过10人不超过20人的部分
超过20人的部分
收费标准
原价(不优惠)
3500元/人
3000元/人
(1)、如果一开始参加旅游的人数为13人,则预计总费用为元;(2)、在(1)问前提下,后来又有部分同学要求参加,设这部分同学加入后总共参与旅游的人数为 人,若总人数 还是不超过20人,则总费用为元;若总人数 超过了20人,则总费用为元;(结果均用含 的代数式表示)(3)、若最后家委会支付给旅行社人均费用为原价的九折,问共有多少人参加了本次旅游?23. 已知 是直线 上的一点, 是直角, 平分 .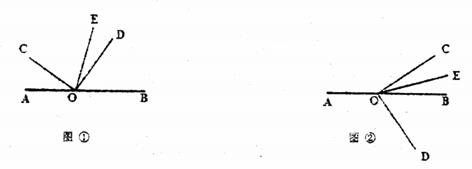 (1)、如图①,若 ,求 的度数;(2)、在图①中,若 ,直接写出 的度数(用含 的代数式表示);(3)、在(1)问前提下 绕顶点 顺时针旋转一周.
(1)、如图①,若 ,求 的度数;(2)、在图①中,若 ,直接写出 的度数(用含 的代数式表示);(3)、在(1)问前提下 绕顶点 顺时针旋转一周.①当旋转至图②的位置,写出 和 的度数之间的关系,并说明理由;
②若旋转的速度为每秒 ,几秒后 ?(直接写出答案)