浙江省杭州市西湖区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $0.01 ， \sqrt{15} ， - 5 ， - \frac{1}{5}$ 这四个数中,无理数的是（）

A、 $0.01$ B、 $\sqrt{15}$ C、 $- 5$ D、 $- \frac{1}{5}$

查看试题解析
2. 下列四种运算中，结果最大的是（）

A、1+(-2) B、1-(-2) C、1×(-2) D、1 $\div$ (-2)

查看试题解析
3. 地球上海洋的面积约为361 000 000平方千米，用科学记数法表示为（）平方千米．

A、361×10⁶ B、36.1×10⁷ C、3.61×10⁸ D、3.61×10⁹

查看试题解析
4. “x的 $\frac{1}{2}$ 与y的和”用代数式可以表示为 $()$

A、 $\frac{1}{2} (x + y)$ B、 $x + \frac{1}{2} + y$ C、 $x + \frac{1}{2} y$ D、 $\frac{1}{2} x + y$

查看试题解析
5. 如果单项式 $2 x^{3} y^{4}$ 与 $- 2 x^{a} y^{2 b}$ 是同类项,那么 $a 、 b$ 的值分别是（）

A、3，2 B、2，2 C、3，4 D、2，4

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt[3]{- 8}$ ＝﹣2 C、 $\sqrt[3]{\frac{125}{64}} = \frac{5}{8}$ D、（﹣2）³×（﹣3）²＝72

查看试题解析
7. 通过估算，估计 $\sqrt{76}$ 的大小应在（）

A、7～8之间 B、8.0～8.5之间 C、8.5～9.0之间 D、9～10之间

查看试题解析
8. 如图，在数轴上有 $a 、 b$ 两个有理数，则下列结论中，正确的是（）

A、 $a + b > 0$ B、 $a - b < 0$ C、 $a • b > 0$ D、 ${(- \frac{a}{b})}^{3} > 0$

查看试题解析
9. 某人以每小时5千米的速度从家步行到单位上班,下班时以每小时4千米的速度按原路返回,结果发现下班路上所花的时间比上班路上所花的时间多10分钟,如果设上班路上所花的时间为 $x$ 小时,则下列根据题意所列方程正确的是（）

A、 $5 x = 4 (x + \frac{1}{6})$ B、 $5 (x + \frac{1}{6}) = 4 x$ C、 $5 (x - \frac{1}{6}) = 4 x$ D、 $5 x = 4 (x - 10)$

查看试题解析
10. 已知点C是线段AB延长线上的一点，M、N分别是线段AB、AC的中点，若MN=4cm，且AB= $\frac{3}{4}$ AC，则线段AC的长为（）cm

A、24 B、32 C、40 D、48

查看试题解析

二、填空题

11. 计算:|-2019|= ， (-1)²⁰¹⁹= .

查看试题解析
12. 一个角的补角等于这个角的3倍，则这个角的度数为.

查看试题解析
13. 当 $a = 100$ 时,代数式 $1.5 (1 - 20 %) a + (1 + 40 %) a =$ .

查看试题解析
14. 整式 $m x + 2 n$ 的值随 $x$ 的取值不同而不同，下表是当 $x$ 取不同值时对应的整式值，则关于 $x$ 的方程 $- m x - 2 n = 4$ 的解为.

查看试题解析
15. 如图，直线AB、CD相交于点O，OE平分∠AOD，OF⊥OC，∠1与∠3的度数之比为3：4，则∠EOC= ， ∠2=.

查看试题解析
16. 在数学拓展课上，小林发现折叠长方形纸片ABCD可以进行如下操作：①把△ABF翻折，点B落在CD边上的点E处，折痕为AF，点F在BC边上；②把△ADH翻折，点D落在AE边上的点G处，折痕为AH，点H在CD边上.若AD=6，AB= $20 - a (0 < a < 14) ，$ 则∠HAF= ， GE=.

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{1}{7} + (- 2) - (- \frac{6}{7})$

(2)、 $\sqrt{36} \div (\frac{2}{3} - \frac{1}{2}) + {(- 2)}^{3}$

查看试题解析
18. 解下列方程：

(1)、 $3 - (4 x - 3) = 7$

(2)、 $\frac{x}{5} - \frac{3 - 2 x}{2} = x$

查看试题解析
19. 如图，已知线段DA与B、C两点，用圆规和无刻度的直尺按下列要求画图并计算：

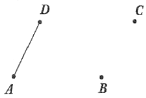(1)、画直线AB、射线DC；

(2)、延长线段DA至点E，使AE=AB(保留作图痕迹)；

(3)、若AB=4cm，AD=2cm，求线段DE的长.

查看试题解析
20. 先化简，再求值:

(1)、已知 $a = - 1 ， b = - 2 ，$ 求 $(6 a^{2} + 4 a b) - 2 (3 a^{2} + a b - \frac{1}{2} b^{2})$ 的值；

(2)、已知 $x^{2} - x y = - 3 ， 2 x y - y^{2} = - 8 ，$ 求 $2 x^{2} + 4 x y - 3 y^{2}$ 的值。

查看试题解析
21. 数轴上点A、B、C所表示的数分别是+4，﹣6，x，线段AB的中点为D.

(1)、求线段AB的长；

(2)、求点D所表示的数；

(3)、若AC＝8，求x的值.

查看试题解析
22. 某工厂加工螺栓、螺帽,已知每1块金属原料可以加工成3个螺栓或4个螺帽(说明:每块金属原料无法同时既加工螺栓又加工螺帽),已知1个螺栓和2个螺帽组成一个零件,为了加工更多的零件,要求螺栓和螺帽恰好配套.请列方程解决下列问题:

(1)、现有20块相同的金属原料,问最多能加工多少个这样的零件?

(2)、若把26块相同的金属原料全部加工完,问加工的螺栓和螺帽恰好配套吗?说明理由

(3)、若把 $n$ 块相同的金属原料全部加工完,为了使这样加工出来的螺栓与螺帽恰好配套,请求出 $n$ 所满足的条件.

查看试题解析
23. 如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB、∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的三倍，则称射线OC是∠AOB的“奇分线”，如图2，∠MPN=42°：

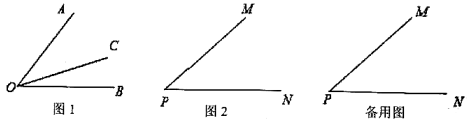(1)、过点P作射线PQ，若射线PQ是∠MPN的“奇分线”，求∠MPQ；

(2)、若射线PE绕点P从PN位置开始，以每秒8°的速度顺时针旋转，当∠EPN首次等于180°时停止旋转，设旋转的时间为 $t$ (秒).当 $t$ 为何值时，射线PN是∠EPM的“奇分线”?

查看试题解析