浙江省东阳市2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2的倒数是（）

A、﹣2 B、2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 据科学家估计，地球的年龄大约是4600000000年，将4600000000用科学记数法表示为（　　）

A、4.6×10⁸ B、46×10⁸ C、4.6⁹ D、4.6×10⁹

查看试题解析
3. 下列各数 $\frac{1}{2}$ ， $\sqrt{9}$ ， $\frac{π}{3}$ ，-2 $\sqrt{5}$ ， $\sqrt[3]{16}$ ，0，2.101101110……（每两个0之间依次多一个1）其中是无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 已知∠α是锐角，∠β是钝角，且∠α+∠β=180°，那么下列结论正确的是（）

A、 $∠ α$ 的补角和 $∠ β$ 的补角相等 B、 $∠ α$ 的余角和 $∠ β$ 的补角相等 C、 $∠ α$ 的余角和 $∠ β$ 的补角互余 D、 $∠ α$ 的余角和 $∠ β$ 的补角互补

查看试题解析
5. 若单项式 $x^{2} y^{m - n}$ 与单项式 $- \frac{1}{2} x^{2 m + n} y^{3}$ 是同类项，那么这两个单项式的和是（）

A、 $\frac{1}{2} x^{4} y^{6}$ B、 $\frac{1}{2} x^{2} y^{3}$ C、 $\frac{3}{2} x^{2} y^{3}$ D、 $- \frac{1}{2} x^{2} y^{3}$

查看试题解析
6. 已知一个数的平方是 $\sqrt{16}$ ，则这个数的立方是（）

A、8 B、64 C、8或 $- 8$ D、64或 $- 64$

查看试题解析
7. 如图，两个正方形的面积分别为36，25，两阴影部分的面积分别为a，b（a＞b），则a-b等于（）

A、9 B、10 C、11 D、12

查看试题解析
8. 已知方程2x+k=6的解为正整数，则k所能取的正整数值为（）

A、1 B、2或3 C、3 D、2或4

查看试题解析
9. 在△ABC中，BC=6，AC=3，过点C作CP⊥AB，垂足为P，则CP长的最大值为（）

A、5 B、4 C、3 D、2

查看试题解析
10. 如图，线段AB表示一条对折的绳子，现从P点将绳子剪断.剪断后的各段绳子中最长的一段为30cm.若AP= $\frac{2}{3}$ BP，则原来绳长为（）cm.

A、55cm B、75cm C、55或75cm D、50或75cm

查看试题解析

二、填空题

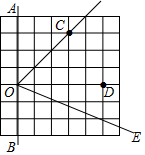
11. 若∠α=39°21′，则∠α的余角为.

查看试题解析
12. 有理数（-1）² ，（-1）³ ， -1² ， |-1|，-（-1），- $\frac{1}{- 1}$ 中，等于1的个数有个.

查看试题解析
13. 如图，在正方形网格中，点O、A、B、C、D均是格点.若OE平分∠BOC，则∠DOE的度数为°.

查看试题解析
14. 当x=2时，代数式ax²+bx+1的值为3，那么当x=-2时，代数式-ax²+bx+1的值是.

查看试题解析
15. 已知两个完全相同的大长方形，长为 $a$ ，各放入四个完全一样的白色小长方形后，得到图①、图②，那么，图①中阴影部分的周长与图②中阴影部分的周长的差是（用含a的代数式表示）.

查看试题解析
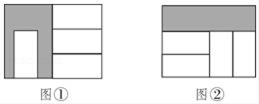16. 已知∠AOB=70°，∠AOD= $\frac{1}{2}$ ∠AOC，∠BOD=3∠BOC（∠BOC＜45°），则∠BOC的度数是.

查看试题解析

三、解答题

17. 计算：

(1)、（-2.4）+ $\frac{6}{5}$ - $\frac{5}{8}$ ×（-4）²+ $\sqrt[3]{- 125}$

(2)、-2²-|-7|+3+2×（- $\frac{1}{2}$ ）

查看试题解析
18. 解方程：

(1)、3x-2=1-2（x+1）；

(2)、 $\frac{x + 4}{5} + 1 = x - \frac{x - 5}{3}$ .

查看试题解析
19. 先化简，再求值：已知x= $\sqrt{3}$ ，y=-2，求代数式2（ $\frac{1}{2}$ x²-3xy-y²）-（2x²-6xy-y²）的值.

查看试题解析
20. 小明准备完成题目：化简：（□x²+6x+8）-（6x+5x²+2）发现系数“□”印刷不清楚.

(1)、她把“□”猜成4，请你化简（4x²+6x+8）-（6x+5x²+2）；

(2)、他妈妈说：“你猜错了，我看到该题标准答案的结果是常数.”请通过计算说明原题中“□”是几？

查看试题解析
21. 已知数轴上有A、B、C三个点对应的数分别是a、b、c，且满足|a+24|+|b+10|+（c-10）²=0；动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒.

(1)、求a、b、c的值；

(2)、若点P到A点距离是到B点距离的2倍，求点P的对应的数；

(3)、当点P运动到B点时，点Q从A点出发，以每秒2个单位的速度向C点运动，Q点到达C点后.再立即以同样的速度返回，运动到终点A，在点Q开始运动后第几秒时，P、Q两点之间的距离为8？请说明理由.

查看试题解析
22. 如图，直线AB，CD相交于点O，OE平分∠BOC，OF⊥OE，且∠AOC=114°，求∠BOF的度数.

查看试题解析
23. 小明和小慧两位同学在数学活动课中，把长为30cm，宽为10cm的长方形白纸条粘合起来，小明按如图甲所示的方法粘合起来得到长方形ABCD，粘合部分的长度为6cm，小慧按如图乙所示的方法粘合起来得到长方形A₁B₁C₁D₁ ，黏合部分的长度为4cm.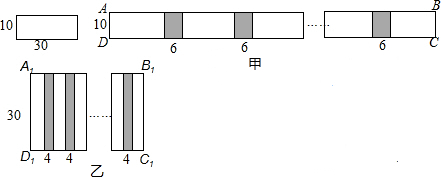

(1)、若按小明或小慧的两种方法各粘贴n张，所得的长方形长AB为， A₁B₁为（用含n的代数式表示）

(2)、若长为30cm，宽为10cm的长方形白纸条共有100张，求小明应分配到多少张长方形白纸条，才能使小明和小慧按各自要求黏合起来的长方形面积相等（要求100张长

查看试题解析
24. 东东在研究数学问题时遇到一个定义：将三个已经排好顺序数：x₁ ， x₂ ， x₃ ，称为数列x₁ ， x₂ ， x₃.计算|x₁|， $\frac{| x_{1} + x_{2} |}{2}$ ， $\frac{| x_{1} + x_{2} + x_{3} |}{3}$ ，将这三个数的最小值称为数列x₁ ， x₂ ， x₃的最佳值.例如，对于数列2，-1，3，因为|2|=2， $\frac{| 2 + (- 1) |}{2}$ = $\frac{1}{2}$ ， $\frac{| 2 + (- 1) + 3 |}{3}$ = $\frac{4}{3}$ ，所以数列2，-1，3的最佳值为 $\frac{1}{2}$ .
东东进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1，2，3的价值为 $\frac{1}{2}$ ；数列3，-1，2的最佳值为1；….经过研究，东东发现，对于“2，-1，3”这三个数，按照不同的排列顺序得到的不同数列中，最佳值的最小值为 $\frac{1}{2}$ .根据以上材料，回答下列问题：

(1)、数列-4，-3，1的最佳值为；

(2)、将“-4，-3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的最佳值的最小值为，取得最佳值最小值的数列为（写出一个即可）；

(3)、将2，-9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列.若这些数列的最佳值为1，求a的值.

查看试题解析