广西来宾市2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元一次方程的是 $($ $)$

A、 $x + 3 = y + 2$ B、 $x + 4 = 3 - x$ C、 $\frac{1}{x} = 1$ D、 $x^{2} - 1 = 0$

查看试题解析
2. “x的 $\frac{1}{2}$ 与y的和”用代数式可以表示为 $()$

A、 $\frac{1}{2} (x + y)$ B、 $x + \frac{1}{2} + y$ C、 $x + \frac{1}{2} y$ D、 $\frac{1}{2} x + y$

查看试题解析
3. 在国家“一带一路”倡议下，我国与欧洲开通了互利互惠的中欧专列.行程最长，途经城市和国家最多的一趟专列全程长13000 km，将13000用科学记数法表示应为（）

A、0.13×10⁵ B、1.3×10⁴ C、1.3×10⁵ D、13×10³

查看试题解析
4. 一个正方体的表面展开图如图所示，已知正方体的每一个面都有一个有理数，且相对面上的两个数互为相反数，那么代数式 $\frac{a}{c} + b$ 的值等于 $($ $)$

A、 $- 6$ B、 $- \frac{3}{4}$ C、 $\frac{3}{4}$ D、6

查看试题解析
5. 下列判断错误的是（　　）

A、多项式5x²﹣2x+4是二次三项式 B、单项式﹣a²b³c⁴的系数是﹣1，次数是9 C、式子m+5，ab，x=1，﹣2， $\frac{s}{v}$ 都是代数式 D、当k=3时，关于x，y的代数式（﹣3kxy+3y）+（9xy﹣8x+1）中不含二次项

查看试题解析
6. 若方程 $2 x + a = 3$ 与方程 $3 x + 1 = 7$ 的解相同，则a的值为 $($ $)$

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
7. 如图，点O在直线AB上， $∠ AOC$ 与 $∠ AOD$ 互余，OE平分 $∠ DOB$ ， $∠ DOE = 75^{\circ}$ ，则 $∠ AOC$ 的度数为 $($ ）

A、 $40^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $70^{\circ}$

查看试题解析
8. 某厂生产上第世博会吉祥物：“海宝”纪念章10万个，质检部门为检测这批纪念章质量的合格情况，从中随机抽查500个，合格499个 $.$ 下列说法正确的是 $($ ）

A、总体是10万个纪念章的合格情况，样本是500个纪念章的合格情况 B、总体是10万个纪念章的合格情况，样本是499个纪念章的合格情况 C、总体是500个纪念章的合格情况，样本是500个纪念章的合格情况 D、总体是10万个纪念章的合格情况，样本是1个纪念章的合格情况

查看试题解析
9. 有理数a、b在数轴上的位置如图所示，则化简 $| a - b | + | a + b |$ 的结果为 $($ $)$

A、 $- 2 a$ B、2b C、2a D、 $- 2 b$

查看试题解析
10. 计算： $2^{1} - 1 = 1$ ， $2^{2} - 1 = 3$ ， $2^{3} - 1 = 7$ ， $2^{4} - 1 = 15$ ， $2^{5} - 1 = 31$ ， $\dots$ 归纳各计算结果中的个位数字规律，猜测 $2^{2018} - 1$ 的个位数字是 $($ $)$

A、1 B、3 C、7 D、5

查看试题解析
11. 下面四个整式中，不能表示图中阴影部分面积的是（）

A、 $(x + 3) (x + 2) - 2 x$ B、 $x (x + 3) + 6$ C、 $3 (x + 2) + x^{2}$ D、 $x^{2} + 5 x$

查看试题解析
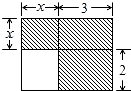12. 某商店老板销售一种商品，他要以不低于进价20%的利润出售，但为了获得更多的利润，他以高出进价80%的价格标价，若你想买下标价为360元的这种商品，商店老板让价的最大限度为（）

A、82元 B、100元 C、120元 D、160元

查看试题解析

二、填空题

13. 若 $y = - 2$ 是方程 $ky - 7 = 3$ 的解，则 $k =$ .

查看试题解析
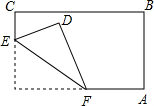
14. 一个角等于它的余角的 $\frac{1}{4}$ ，则这个角的补角的度数是.

查看试题解析
15. 已知a²+a=1，则代数式3﹣a﹣a²的值为.

查看试题解析
16. 拿一张长方形纸片，按图中所示的方法折叠一角，得到折痕EF，如果 $∠ DFE = 36^{\circ}$ ，则 $∠ DFA =$ .

查看试题解析
17. 一旅客携带了30千克行李乘飞机，按民航规定，旅客最多可免费携带20千克行李，超出部分每千克按飞机票价的 $1.5 %$ 购买行李票，该旅客此次机票与行李票共花了920元，则他的飞机票价是元 $.$

查看试题解析
18. 操场上站成一排的100名学生进行报数游戏，规则是：每人依次报自己的顺序数的倒数加1，如：第一人报 $(\frac{1}{1} + 1)$ ，第二人报 $(\frac{1}{2} + 1)$ ，第三人报 $(\frac{1}{3} + 1)$ ， $\dots$ ，第100人报 $(\frac{1}{100} + 1)$ ，这样得到的100个数的积为.

查看试题解析

三、解答题

19. 计算： $- {(- 4)}^{2} - (- 2^{4} - 5^{2} \times 3) \div (- 7)$ .

查看试题解析
20. 解方程： $\frac{5 x - 7}{6} + 1 = \frac{3 x - 1}{4}$ ．

查看试题解析
21. 先化简，再求值： $2 (5 a^{2} - 7 a b + 9 b^{2}) - 3 (14 a^{2} - 2 a b + 3 b^{2})$ ，其中 $a = \frac{3}{4}$ ， $b = - \frac{2}{3}$ .

查看试题解析
22. 如果一个足球的质量以400克为标准，用正数记超过标准质量的克数，用负数记不足标准质量的克数 $.$ 下面是5个足球的质量检测结果 $($ 单位：克 $)$ ： $- 25$ ， $+ 10$ ， $- 20$ ， $+ 30$ ， $+ 15$ .

(1)、写出这5个足球的质量；

(2)、请指出选用哪一个足球好些，并用绝对值的知识进行说明.

查看试题解析
23. 某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、合格、优秀，并绘制成如下的不完全统计图.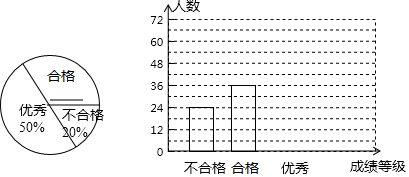

请你根据图中所给的信息解答下列问题：

(1)、请将以上两幅统计图补充完整；

(2)、若“合格”和“优秀”均视为达标成绩，求该校被抽取的学生中的达标人数；

(3)、若该校有学生1200人，请你估计此次测试中，全校达标的学生人数.

查看试题解析
24. 已知线段 $A B = 14$ ，在线段AB上有点C，D，M，N四个点，且满足AC：CD： $D B = 1$ ：2：4， $A M = \frac{1}{2} A C$ ，且 $D N = \frac{1}{4} B D$ ，求MN的长.

查看试题解析
25. 某开发公司要生产若干件新产品，需要精加工后，才能投放市场，现有红星和巨星两家加工厂都想加工这批产品，已知红星厂单独加工比巨星厂单独加工这批产品多用20天，红星厂每天可加工16件产品，巨星厂每天可加工24件产品，公司需付给红星厂每天加工费800元，付给巨星厂每天加工费1200元.

(1)、这个公司要加工多少件新产品？

(2)、公司的产品可由一家工厂单独加工完成，也可由两家工厂合作完成，在加工过程中公司需另派一名工程师每天到厂家进行指导，并支付工程师每天10元的午餐补助，请你帮助公司从所有可供选择的方案中，选择一种既省钱又省时的加工方案.

查看试题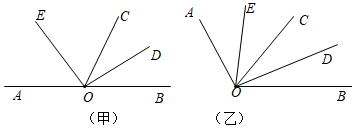解析
26. 如图

(1)、如图 $($ 甲 $)$ ，点O在直线AB上，OC为射线，OD，OE分别平分 $∠ B O C$ ， $∠ A O C$ .
$①$ 若 $∠ B O C = 40^{\circ}$ ， $∠ C O D$ 与 $∠ C O E$ 有怎样的数量关系？说明理由；

$②$ 若 $∠ B O C = α (α < 180^{\circ})$ ， $∠ C O D$ 与 $∠ C O E$ 又有怎样的数量关系？说明理由；

(2)、如图 $($ 乙 $)$ ， $∠ A O B = 120^{\circ}$ ，OC为 $∠ A O B$ 内的一条射线， $∠ B O C = α (α < 120^{\circ})$ ，OD，OE分别平分 $∠ B O C$ ， $∠ A O C$ ， $(1)$ 中的结论是否还成立？若不成立，直接写出正确的结论.

查看试题解析