广西防城港市2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 8的倒数是（）

A、 ﹣8 B、8 C、﹣ $\frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 中共十九大召开期间，十九大代表纷纷利用休息时间来到北京展览馆，参观“砥砺奋进的五年”大型成就展，据统计，9月下旬开幕至10月22日，展览累计参观人数已经超过78万，请将780000用科学记数法表示为（）

A、78×10⁴ B、7.8×10⁵ C、7.8×10⁶ D、0.78×10⁶

查看试题解析
3. 汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是（）

A、点动成线 B、线动成面 C、面动成体 D、以上答案都不对

查看试题解析
4. 单项式2a³b的次数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 要整齐地栽一行树，只要确定两端的树坑的位置，就能确定这一行树坑所在的直线，这里用到的数学知识是（）

A、两点之间的所有连线中，线段最短 B、经过两点有一条直线，并且只有一条直线 C、直线外一点与直线上各点连接的所有线段中，垂线段最短 D、经过一点有且只有一条直线与已知直线垂直

查看试题解析
6. 下列各式合并同类项结果正确的是（）

A、3x²﹣x²=3 B、3a²﹣a²=2a² C、3a²﹣a²=a D、3x²+5x³=8x⁵

查看试题解析
7. 下列等式变形正确的是（）

A、若﹣3x＝5，则x＝ $- \frac{3}{5}$ B、若 $\frac{x}{3} + \frac{x - 1}{2} = 1$ ，则2x+3（x﹣1）＝1 C、若5x﹣6＝2x+8，则5x+2x＝8+6 D、若3（x+1）﹣2x＝1，则3x+3﹣2x＝1

查看试题解析
8. 如图，甲从A点出发向北偏东70°方向走到点B，乙从点A出发向南偏西15°方向走到点C，则∠BAC的度数是（）

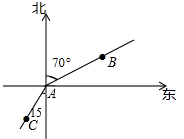A、85° B、105° C、125° D、160°

查看试题解析
9. 已知 $k = \frac{4 x + 3}{2 x - 1}$ ，则满足 $k$ 为整数的所有整数 $x$ 的和是（）．

A、-1 B、0 C、1 D、2

查看试题解析
10. 如图，OC为 $∠ AOB$ 内一条直线，下列条件中不能确定OC平分 $∠ AOB$ 的是 $()$

A、 $∠ AOC = ∠ BOC$ B、 $∠ AOB = 2 ∠ AOC$ C、 $∠ AOC + ∠ COB = ∠ AOB$ D、 $∠ BOC = \frac{1}{2} ∠ AOB$

查看试题解析
11. 商店对某种手机的售价作了调整，按原售价的 8 折出售，此时的利润率为 14%，若此种手机的进价为 1200 元，设该手机的原售价为 x 元，则下列方程正确的是（）

A、0.8x﹣1200＝1200×14% B、0.8x﹣1200＝14%x C、x﹣0.8x＝1200×14% D、0.8x﹣1200＝14%×0.8x

查看试题解析
12. 下列说法正确的有（）
①一个数不是正数就是负数；②海拔-155 m表示比海平面低155 m；③负分数不是有理数；④零是最小的数；⑤零是整数，也是正数.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 比较大小：-30.（填“< ”“=”“ > ”）

查看试题解析
14. 如果 $\frac{7}{5}$ x³ⁿy^m⁺⁴与﹣3x⁶y²ⁿ是同类项，那么mn的值为．

查看试题解析
15. 25°的角的余角的度数与它的补角的度数的比是.

查看试题解析
16. 泰兴某企业有 $m$ 吨煤，计划用 $n$ 天，为积极响应市政府“节能减排”的号召，现打算多用 $5$ 天，则现在比原计划每天少用煤吨.

查看试题解析
17. 若有理数a，b，c在数轴上的位置如图所示，则化简： $| a + c | + | 2 a + b | - | c - b | =$ ．

查看试题解析
18. 按一定顺序排列的一列数叫做数列，如数列： $\frac{1}{2}$ ， $\frac{1}{6}$ ， $\frac{1}{12}$ ， $\frac{1}{20}$ ，…，则这个数列前2018个数的和为．

查看试题解析

三、解答题

19. 计算：[(﹣1)²⁰¹⁵﹣( $\frac{1}{4} - \frac{1}{6} - \frac{3}{8}$ )×24]÷|﹣3²+5|.

查看试题解析
20. 如图，已知四点 A，B，C，D，请按要求画图

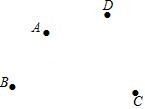
①画直线 AB，射线 CD 交于点 M

②连接 AC，BD 交于点 N

③连接 MN，并延长至点 E，使 NE＝NM.

查看试题解析
21. 解方程：

(1)、10x﹣12＝5x+15；

(2)、 $\frac{1}{3} [x - \frac{1}{2} (x - 1)] = \frac{2}{3} (x - \frac{1}{2})$

查看试题解析
22. 如图1，已知点C在线段AB上，线段AC=10厘米，BC=6厘米，点M，N分别是AC，BC的中点.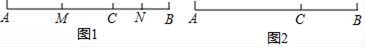

(1)、求线段MN的长度；

(2)、根据第（1）题的计算过程和结果，设AC+BC=a，其他条件不变，求MN的长度；

(3)、动点P、Q分别从A、B同时出发，点P以2cm/s的速度沿AB向右运动，终点为B，点Q以1cm/s的速度沿AB向左运动，终点为A，当一个点到达终点，另一个点也随之停止运动，求运动多少秒时，C、P、Q三点有一点恰好是以另两点为端点的线段的中点？

查看试题解析
23. 先化简，再求值：（2x²﹣2y²）﹣3（x²y²+x²）+3（x²y²+y²），其中x＝﹣1，y＝2.

查看试题解析
24. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

(1)、接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析
25. 如图，已知∠AOC＝∠BOD＝70°，∠BOC＝31°，求∠AOD 的度数.

查看试题解析
26. 列代数式或方程：

(1)、a与b的平方和；

(2)、m的2倍与n的差的相反数；

(3)、某校女生占全体学生数的52%，比男生多80人，这个学校有多少学生？（设男生人数为x人）

查看试题解析