浙江省衢州市2019届九年级上学期数学期中考试试卷
试卷更新日期:2019-08-05 类型:期中考试
一、单选题
-
1. 有五张背面完全相同的卡片,正面分别写有数字1,2,3,4,5,把这些卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是偶数的概率为( )A、 B、 C、 D、2. ⊙O以原点为圆心,5为半径,点P的坐标为(4,2),则点P与⊙O的位置关系是( )A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、点P在⊙O上或⊙O外3. 某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
 A、抛一枚硬币,出现正面朝上 B、掷一个正六面体的骰子,出现3点朝上 C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球4. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、5. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则( )
A、抛一枚硬币,出现正面朝上 B、掷一个正六面体的骰子,出现3点朝上 C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球4. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、5. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则( )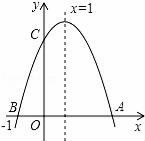
①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是
A、1 B、2 C、3 D、46. 如图,⊙A过点O(0,0),C( ,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )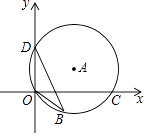 A、15° B、30° C、45° D、60°7. 如图,已知四边形ABCD内接于⊙O,连结BD,∠BAD=105°,∠DBC=75°.若⊙O的半径为3,则弧BC的长是( )
A、15° B、30° C、45° D、60°7. 如图,已知四边形ABCD内接于⊙O,连结BD,∠BAD=105°,∠DBC=75°.若⊙O的半径为3,则弧BC的长是( )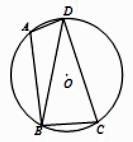 A、 B、π C、 D、8. 如图,△ABC中,∠C=90°,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则BE的长为( )
A、 B、π C、 D、8. 如图,△ABC中,∠C=90°,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则BE的长为( )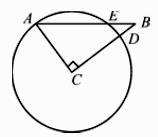 A、 B、 C、 D、9. 四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、 B、 C、 D、9. 四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、甲 B、乙 C、丙 D、丁10. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018 , 如果点A的坐标为( ,0),那么点B2018的坐标为( )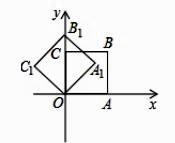 A、(1,1) B、(0, ) C、(﹣1,1) D、(- ,0)
A、(1,1) B、(0, ) C、(﹣1,1) D、(- ,0)二、填空题
-
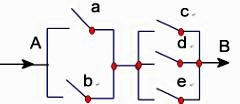
11. 如图所示,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是.
 12. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣ .在飞机着陆滑行中,最后4s滑行的距离是m.13. 如图,AB是⊙O的直轻,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA=.
12. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣ .在飞机着陆滑行中,最后4s滑行的距离是m.13. 如图,AB是⊙O的直轻,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA=.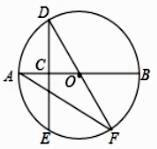 14. 如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为.
14. 如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为.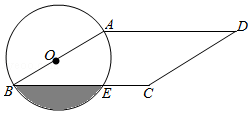 15. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为;点E在运动过程中,线段FG的长度的最小值为.
15. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为;点E在运动过程中,线段FG的长度的最小值为. 16. 将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象.P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t=.
16. 将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象.P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t=.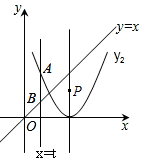
三、解答题
-
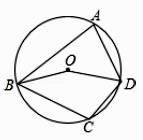
17. 如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
 18. 某同学报名参加校运会,有以下5个项目可供选择:径赛项目:100m,200m,400m(分别用A1 , A2 , A3表示);田赛项目:跳远,跳高(分别用B1 , B2表示)(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率是多少?(2)、该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求出恰好是1个田赛项目和1个径赛项目的概率.19. 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
18. 某同学报名参加校运会,有以下5个项目可供选择:径赛项目:100m,200m,400m(分别用A1 , A2 , A3表示);田赛项目:跳远,跳高(分别用B1 , B2表示)(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率是多少?(2)、该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求出恰好是1个田赛项目和1个径赛项目的概率.19. 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°. (1)、求∠DAB的度数;(2)、求图中阴影部分的面积(结果保留π)20. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)、求∠DAB的度数;(2)、求图中阴影部分的面积(结果保留π)20. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).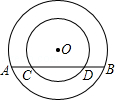 (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.21. 某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.21. 某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)、求y与x之间的函数关系式;
(2)、设该护肤品的日销售利润为w(元),当销售单价x为多少时,日销售利润w最大,最大日销售利润是多少?
22. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.
(1)、求抛物线y=x2﹣2x+2与x轴的“和谐值”;(2)、求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”;(3)、求抛物线y=x2﹣2x+2在抛物线 的上方,且两条抛物线的“和谐值”为2,求c的值.23. 已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.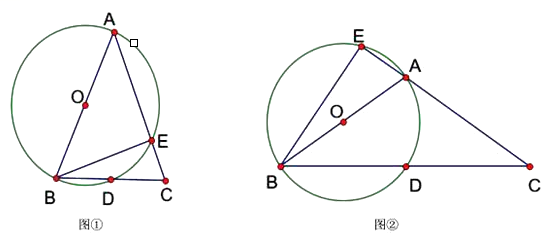 (1)、当∠BAC为锐角时,如图①,求证:∠CBE= ∠BAC;(2)、当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.24. 对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:(1)、(尝试)
(1)、当∠BAC为锐角时,如图①,求证:∠CBE= ∠BAC;(2)、当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.24. 对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:(1)、(尝试)当t=2时,抛物线y=t(x2-3x+2)+(1-t)(-2x+4)的顶点坐标为;
(2)、判断点A是否在抛物线L上;(3)、求n的值.(4)、(发现)通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为.(5)、(应用)二次函数y=-3x2+5x+2是二次函数y=x23x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.