浙江省金华市2019届九年级上学期数学期中考试试卷
试卷更新日期：2019-08-05 类型：期中考试
一、单选题
-
1. 已知⊙O的直径为4cm，点P与圆心O之间的距离为4cm，那么点P与⊙O的位置关系为（ ）
A、在圆上 B、在圆内 C、在圆外 D、不能确定2. 抛物线y=3（x﹣2）2+5的顶点坐标是（ ）A、（﹣2，5） B、（﹣2，﹣5） C、（2，5） D、（2，﹣5）3. 任意掷一枚骰子，下列情况出现的可能性比较大的是（ ）
A、面朝上的点数是3 B、面朝上的点数是奇数 C、面朝上的点数小于2 D、面朝上的点数不小于34. 四边形ABCD内接于⊙O，则∠A:∠B:∠C:∠D的值可以是（ ）A、2:3:4:5 B、2:4:3:5 C、2:5:3:4 D、2:3:5:45. 小东是一名职业足球队员，根据以往比赛数据统计，小东进球率为8%，他明天将参加一场比赛，下面几种说法正确的是（ ）
A、小东明天每射球8次必进球1次 B、小东明天的进球率为8% C、小东明天肯定进球 D、小东明天有可能进球6. 如图，已知圆心角∠AOB=118°，则圆周角∠ACB=（ ）
A、59° B、118° C、121° D、125°7. 已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（ ）
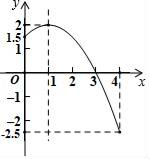A、有最大值2，有最小值﹣2.5 B、有最大值2，有最小值1.5 C、有最大值1.5，有最小值﹣2.5 D、有最大值2，无最小值8. 从1，2，3，4，5这5个数中任取2个，它们的和是偶数的概率是（ ）
A、 B、 C、 D、以上都不对9. 如图，已知⊙O的半径是4，点A，B，C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（ ）
A、 B、 C、 D、二、解答题
-
10. 已知抛物线y=﹣2x2+4x+1．
(1)、求这个抛物线的对称轴和顶点坐标；
(2)、将这个抛物线平移，使顶点移到点P(－2，0)的位置，写出所得新抛物线的表达式和平移的过程．
11. 已知一个口袋中装有9个只有颜色不同的球，其中4个白球，5个红球.(1)、求从中随机抽取出一个红球的概率是多少？(2)、若往口袋中再放入x个白球和y个红球，从口袋中随机取出一个白球的概率是 .求y与x之间的函数关系式.12. 已知：如图，A，B，C，D是⊙O上的点，且AB=CD，求证：∠AOC=∠BOD.
13. 已知某校乒乓球队有水平相当的A，B，C，D四名队员．(1)、若将A，B，C，D四名队员随机平均分成甲、乙两组进行乒乓球单打练习，求A、B恰好分在一组的概率．
(2)、若从A，B，C，D四名队员中随机抽取两名代表学校参加比赛，求A、B恰好被抽中的概率
14. 如图是由边长为1的小正方形组成的10×5网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点B按下列步骤移动第一步：点B绕点A逆时针旋转180°得到点B1；第二步：点B1绕点D逆时针旋转90°得到点B2；第三步：点B2绕点C逆时针旋转90°回到点B
(1)、请用圆规画出点B→B1→B2→B经过的路径；(2)、所画图形是图形；(3)、求所画图形的周长（结果保留π）15. 如图，抛物线y=ax2+bx(a＜0）过点E(10，0)，矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上.设A(t，0)，当t=2时，AD=4.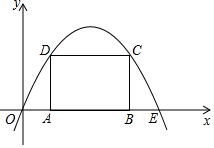
(1)、求抛物线的函数表达式.(2)、当t为何值时，矩形ABCD的周长有最大值？最大值是多少？(3)、保持t=2时的矩形ABCD不动，向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离.16. 若一个四边形的两条对角线互相垂直且相等，则称这个四边形为“奇妙四边形”.如图1，四边形ABCD中，若AC=BD，AC⊥BD，则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质：“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答：
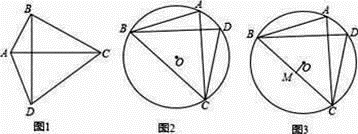(1)、矩形“奇妙四边形”（填“是”或“不是”）；(2)、如图2，已知⊙O的内接四边形ABCD是“奇妙四边形”，若⊙O的半径为6，∠BCD=60°.“奇妙四边形”ABCD的面积为；(3)、如图3，已知⊙O的内接四边形ABCD是“奇妙四边形”，作OM⊥BC于M.请猜测OM与AD的数量关系，并证明你的结论.17. 如图，抛物线y=ax2+bx－3过A(－1，0)、B(3，0)，直线AD交抛物线于点D，点D的横坐标为2，点P(m，n)是线段AD上的动点.
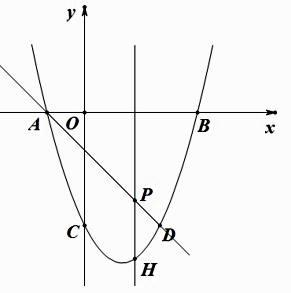(1)、求直线AD及抛物线的解析式.(2)、过点P的直线垂直于x轴，交抛物线于点H，求线段PH的长度l与m的关系式，m为何值时，PH最长？(3)、在平面内是否存在整点（横、纵坐标都为整数）E，使得P、H、D、E为顶点的四边形是平行四边形？若存在，请求出点E的坐标；若不存在，说明理由.三、填空题
-
18. 如果抛物线y=(a﹣1)x2的开口向下，那么a的取值范围是 ．
19. 农历五月初五为端午节，端午节吃粽子是中华民族的传统习俗．小金妈妈买了3个红豆粽、2个碱水粽、5个腊肉粽，粽子除了内部馅料不同外其他均相同．小金随意吃了一个，则吃到红豆棕的概率为 ．
20. 已知一个正多边形的内角是135°，那么这个正多边形的边数是 ．
