浙江省杭州市下城区2019届九年级上学期数学期中考试试卷
试卷更新日期:2019-08-05 类型:期中考试
一、单选题
-
1. 下列函数中,属于二次函数的是( )A、y=2x B、y=﹣2x﹣1 C、y=x2+2 D、y=2. 已知反比例函数y= 的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
 A、
A、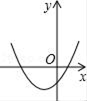 B、
B、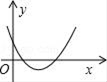 C、
C、 D、
D、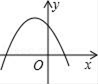 3. 排水管的截面如图,水面宽 ,圆心 到水面的距离 ,则排水管的半径等于( )
3. 排水管的截面如图,水面宽 ,圆心 到水面的距离 ,则排水管的半径等于( ) A、5 B、6 C、8 D、44. 如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A、5 B、6 C、8 D、44. 如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )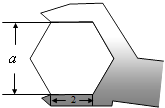 A、 cm B、 cm C、 cm D、1cm5. 给定下列条件可以确定一个圆的是( )A、已知圆心 B、已知半径 C、已知直径 D、不在同一直线上三点6.
A、 cm B、 cm C、 cm D、1cm5. 给定下列条件可以确定一个圆的是( )A、已知圆心 B、已知半径 C、已知直径 D、不在同一直线上三点6.一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )
 A、袋子一定有三个白球 B、袋子中白球占小球总数的十分之三 C、再摸三次球,一定有一次是白球 D、再摸1000次,摸出白球的次数会接近330次7. 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc>0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是( )
A、袋子一定有三个白球 B、袋子中白球占小球总数的十分之三 C、再摸三次球,一定有一次是白球 D、再摸1000次,摸出白球的次数会接近330次7. 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc>0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是( )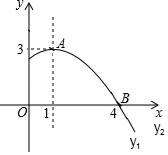 A、②③ B、①③ C、①③④ D、①②③④8. 已知k,n均为非负实数,且2k+n=2,则代数式2k2﹣4n的最小值为( )A、﹣40 B、﹣16 C、﹣8 D、09. 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A、②③ B、①③ C、①③④ D、①②③④8. 已知k,n均为非负实数,且2k+n=2,则代数式2k2﹣4n的最小值为( )A、﹣40 B、﹣16 C、﹣8 D、09. 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )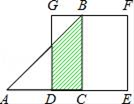 A、
A、 B、
B、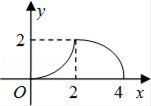 C、
C、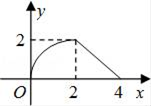 D、
D、 10. 一张圆形纸片,小芳进行了如下连续操作:
10. 一张圆形纸片,小芳进行了如下连续操作:
( 1 )将圆形纸片左右对折,折痕为AB,如图(2)所示.(2)将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图(3)所示.(3)将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图(4)所示.(4)连结AE、AF,如图(5)所示.经过以上操作小芳得到了以下结论:①CD∥EF;②四边形MEBF是菱形;③△AEF为等边三角形;④ ,以上结论正确的有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
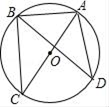
11. 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=40°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是.
 12. 在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些球除标注的数字外完全相同.现从中随机依次取出两个球(不放回),则取出的两个小球标注的数字之和为6的概率是.13. 将函数y=﹣ x2+4x﹣3化为y=a(x﹣m)2+k的形式,得 , 它的图象顶点坐标是.14. 如图,△ABC中,∠ACB=90°,∠A=25°,若以点C为旋转中心,将△ABC旋转θ度到△DEC的位置,使点B恰好落在边DE上,则θ等于.
12. 在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些球除标注的数字外完全相同.现从中随机依次取出两个球(不放回),则取出的两个小球标注的数字之和为6的概率是.13. 将函数y=﹣ x2+4x﹣3化为y=a(x﹣m)2+k的形式,得 , 它的图象顶点坐标是.14. 如图,△ABC中,∠ACB=90°,∠A=25°,若以点C为旋转中心,将△ABC旋转θ度到△DEC的位置,使点B恰好落在边DE上,则θ等于.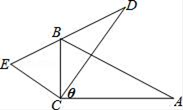 15. 已知圆O的直径为4cm,A是圆上一固定点,弦BC的长为2 cm,当△ABC为等腰三角形时,其底边上的高为.16. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
15. 已知圆O的直径为4cm,A是圆上一固定点,弦BC的长为2 cm,当△ABC为等腰三角形时,其底边上的高为.16. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
三、解答题
-
17. 抽屉里放有4只白袜子和2只黑袜子.(1)、从中任意摸出1只袜子,记下颜色后放回,搅匀,再摸出1只袜子,摸出的两只袜子颜色相同的概率是多少.(2)、若第一次摸出不放回,摸出的两只袜子颜色相同的概率是多少.18. 如图,C,D是以AB为直径的半圆周的三等分点,CD=8cm,P是直径AB上的任意一点.
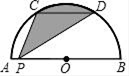 (1)、求 的长;(2)、求阴影部分的面积.19. 已知二次函数的图象经过点A(﹣1,0)和点B(3,0),且有最小值为﹣2.(1)、求这个函数的解析式;(2)、函数的开口方向、对称轴;(3)、当y>0时,x的取值范围.20. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结E C.若AB=8,CD=2.
(1)、求 的长;(2)、求阴影部分的面积.19. 已知二次函数的图象经过点A(﹣1,0)和点B(3,0),且有最小值为﹣2.(1)、求这个函数的解析式;(2)、函数的开口方向、对称轴;(3)、当y>0时,x的取值范围.20. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结E C.若AB=8,CD=2.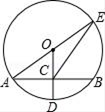 (1)、求OD的长.(2)、求EC的长.21. 实验中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长度为30米的篱笆围成已知墙长18米,设这个苗圃园垂直于墙的一边为x米.
(1)、求OD的长.(2)、求EC的长.21. 实验中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长度为30米的篱笆围成已知墙长18米,设这个苗圃园垂直于墙的一边为x米.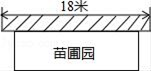 (1)、若平行于墙的一边的长为y米,直接写出y与x之间的函数关系,以及其自变量的取值范围.(2)、若垂直于墙的一边的长不小于8米,当x为多少米时,这个苗圃的面积最大?求出这个最大值.
(1)、若平行于墙的一边的长为y米,直接写出y与x之间的函数关系,以及其自变量的取值范围.(2)、若垂直于墙的一边的长不小于8米,当x为多少米时,这个苗圃的面积最大?求出这个最大值.