浙江省富阳市2019届九年级上学期数学期中考试试卷
试卷更新日期：2019-08-05 类型：期中考试
一、单选题
-
1. 由二次函数 ，可知（ ）A、其图象的开口向下 B、其图象的对称轴为直线 C、当x<3时，y随x的增大而增大 D、其最小值为12. 下列说法正确的是（ ）A、“明天降雨的概率是75％”表示明天有75％的时间都在降雨 B、“抛一枚硬币正面朝上的概率为 ”表示每抛2次就有1次正面朝上 C、“抛一枚均匀的正方体骰子，朝上的点数是2的概率为 ”表示随着抛掷次数的增加，“抛出朝上的点数是2”这一事件发生的频率稳定在 左右 D、“彩票中奖的概率为1％”表示买100张彩票肯定会中奖3. 如图，点A是圆O上一点，BC是圆O的弦，若∠A=50°，则∠OBC的度数（ ）
A、40° B、50° C、25° D、100°4. 已知（﹣2，a），（3，b）是函数y＝﹣4x2+8x+m上的点，则（ ）A、b＜a B、a＜b C、b＝c D、a，b的大小关系不确定5. 在△ABC中，已知AB=AC=8cm，BC=12cm，P是BC的中点，以P为圆心作一个6cm为半径的圆P，则A，B，C三点在圆P内的有（ ）个
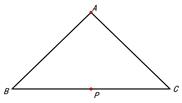A、0 B、1 C、2 D、36. 已知二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，那么关于x的一元二次方程ax2+bx+c=0的两个解为（ ）
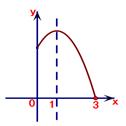A、1，3 B、-2，3 C、-1，3 D、3，47. 四边形ABCD内接于⊙O， ，∠BAD=120°，则∠ABC的度数为（ ）A、100° B、105° C、120° D、125°8. 下列命题中，正确的是（ ）①平面内三个点确定一个圆；②平分弦的直径平分弦所对的弧；③半圆所对的圆周角是直角；④圆的内接菱形是正方形；⑤相等的弧所对的圆周角相等.
A、①②③ B、②④⑤ C、①②⑤ D、③④9. 如图，已知圆O的半径为10，AB⊥CD，垂足为P，且AB＝CD＝16，则OP的长为（ ）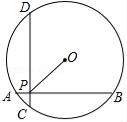
A、6 B、6 C、8 D、810. 已知二次函数y=ax2+bx+c（a＞0）的图象的对称轴为直线x=1，且（x1 ， y1），（x2 ， y2）为其图象上的两点，（ ）A、若x1＞x2＞1，则（y1-y2）+2a（x1-x2）＜0 B、若1＞x1＞x2 ， 则（y1-y2）+2a（x1-x2）＜0 C、若x1＞x2＞1，则（y1-y2）+a（x1-x2）＞0 D、若1＞x1＞x2 ， 则（y1-y2）+a（x1-x2）＞0二、填空题
-
11. 已知扇形所在圆半径为4，弧长为6π，则扇形面积为12. 从长为1，3，4，5的四条线段中任意选出3条，则能组成三角形的概率为13. 某游乐园要建一个圆形喷水池，在喷水池的中心安装一个大的喷水头，高度为 m，喷出的水柱沿抛物线轨迹运动（如图），在离中心水平距离4m处达到最高，高度为6m，之后落在水池边缘，那么这个喷水池的直径AB为m.
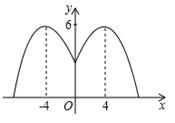14. 如图，点 ， ， ， 在 上， ， ， ，则 .
15. 已知正方形ABCD与正△EFG都内接于圆O，若正方形边长为 ，则EF=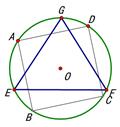
16. 已知关于x的二次函数y=ax2+(a2-1)x-a(a≠0)的图象与x轴的一个交点为(m，0)，若2＜m＜4，则a的范围.三、解答题
-
17. 已知抛物线y=ax2+bx+c(a≠0)的图像经过点（0，1），且当x=2时，函数有最大值为4，(1)、求函数表达式(2)、直接写出：当x取何值时，函数值大于1(3)、写出将函数图象向左平移1个单位，向上平移2个单位后所得到的函数表达式18. 如图，一圆弧形钢梁
(1)、请用直尺和圆规补全钢梁所在圆(2)、若钢梁的拱高为8米，跨径为40米，求这钢梁圆弧的半径。19. 4件同型号的产品中，有1件不合格品和3件合格品．
(1)、从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；
(2)、从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；
(3)、在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？20. 已知矩形ABCD的四个顶点在正△EFG的边上，已知正三角形边长为4，记矩形面积为S，边长FA为x，
(1)、求S的关于x的函数表达式并写出x的取值范围(2)、求S随x增大而增大时自变量x的取值范围，并求出面积的最值21. 平面直角坐标系xOy中，抛物线y=kx2-2k2x-3交y轴于A点，交直线x=-4于B点.
(1)、抛物线的对称轴为直线x=（用含k的代数式表示）；(2)、若AB//x轴，求抛物线的解析式；(3)、当-4<k<0时，记抛物线在A，B之间的部分为图象G（包含A，B两点），若对于图象G上任意一点P（xP ， yP），yP≥-3，结合函数图象写出k的取值范围.22. 如图，在△ABC中，AB＝AC，E在AC上，经过A，B，E三点的圆O交BC于点D，且D点是弧BE的中点，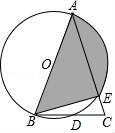
(1)、求证AB是圆的直径；(2)、若AB＝8，∠C＝60°，求阴影部分的面积；(3)、当∠A为锐角时，试说明∠A与∠CBE的关系.23. 在平面直角坐标系中，已知抛物线y1＝x2﹣4x+4的顶点为A，直线y2＝kx﹣2k（k≠0），(1)、试说明直线是否经过抛物线顶点A；(2)、若直线y2交抛物线于点B，且△OAB面积为1时，求B点坐标；(3)、过x轴上的一点M（t，0）（0≤t≤2），作x轴的垂线，分别交y1 ， y2的图象于点P，Q，判断下列说法是否正确，并说明理由：①当k＞0时，存在实数t（0≤t≤2）使得PQ＝3.
②当﹣2＜k＜﹣0.5时，不存在满足条件的t（0≤t≤2）使得PQ＝3.