浙江省台州市三门县2019届九年级上学期数学期末考试试卷
试卷更新日期：2019-08-05 类型：期末考试
一、单选题
-
1. 反比例函数y=的图象在（ ）A、第一，二象限 B、第一，三象限 C、第二，四象限 D、第三，四象限2. 下列剪纸作品中是中心对称图形的是（ ）A、
B、
C、
D、
3. 将 向上平移2个单位后所得的抛物线的解析式为（ ）A、 B、 C、 D、4. 下列说法中，正确的是（ ）A、不可能事件发生的概率为0 B、随机事件发生的概率为 C、“明天要降雨的概率为 ”，表示明天有半天时间都在降雨 D、投掷一枚质地均匀的硬币100次，正面朝上的次数一定为50次5. 如图，A，B是⊙O上的两点，C是⊙O上不与A，B重合的任意一点.如果∠AOB＝130°，那么∠ACB的度数为（ ）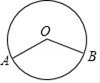
A、65° B、115° C、130° D、65°或115°6. 对于二次函数y＝﹣2(x+1)(x﹣3)，下列说法正确的是（ ）A、图象与x轴的交点为(1，0)，(﹣3，0) B、图象的对称轴是直线x＝﹣2 C、当x＜1时，y随x的增大而增大 D、此函数有最小值为87. 如图，把矩形ABCD绕点A顺时针旋转，使点B的对应点B落在DA的延长线上，若AB＝2，BC＝4，则点C与其对应点C的距离为（ ）
A、6 B、8 C、2 D、28. 有x支球队参加篮球比赛，每两队之间都比赛一场，共比赛了21场，则下列方程中符合题意的是（ ）A、x（x﹣1）＝21 B、x（x﹣1）＝42 C、x（x+1）＝21 D、x（x+1）＝429. 如图，在平面直角坐标系中，双曲线y＝ ，y＝﹣ 与⊙O相交，以交点为顶点的八边形ABCDEFGH是正八边形，则此正八边形的面积为（ ）
A、32 B、64 C、16 D、16+1610. 如图，抛物线y＝ax2+bx+c(a≠0)与y轴交于点C，与x轴交于A，B两点，其中点B的坐标为B(4，0)，抛物线的对称轴交x轴于点D，CE∥AB，并与抛物线的对称轴交于点E现有下列结论：①b2﹣4a＜0；②b＞0；③5a+b＜0；④AD+CE＝4.其中正确结论个数为（ ）
A、4 B、3 C、2 D、1二、填空题
-
11. 点M(1，2)关于原点的对称点的坐标为.12. 小红在一次班会中参与学科知识抢答活动，现有语文题6个，数学题5个，英语题9个，她从中随机抽取1个，抽中数学题的概率是 .
13. 已知函数的图象经过点(1，3)，且与x轴没有交点，写出一个满足题意的函数的解析式.14. 在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在墙壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”问题题意为：如图，有一圆柱形木材埋在墙壁中，不知其直径大小.用锯去锯这木材，锯口深1寸(即CD＝1寸)，锯道长1尺(即AB＝1尺)，问这圆形木材直径是多少？(注：1尺＝10寸)由此，可求出这圆形木材直径为寸.
15. 我县在治理违建的过程中，某小区拆除了自建房，改建绿地.如图，自建房占地是边长为20m的正方形ABCD，改建的绿地是矩形AEFG，其中点E在AB上，点G在AD的延长线上，且DG＝2BE.如果设BE的长为x(单位：m)，绿地AEFG的面积为y(单位：m2)，那么y与x的函数的解析式为 ， 绿地AEFG的最大面积为m2.
16. 如图，四边形ABCD是⊙O的内接四边形，AC为直径，点B是弧AC的中点，若AC＝7，BD＝6，则由四个弓形组成的阴影部分的面积为.
三、解答题
-
17. 解方程：(1)、x2﹣9＝0(2)、x2+8x﹣20＝018. 在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型.如图，已知△ABC是腰长为16cm的等腰直角三角形.
(1)、在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形(要求：尺规作图，保留作图痕迹，不写作法)；(2)、请求出所制作圆锥底面的半径长.19. 如图，在平面直角坐标系xOy中，直线y＝x+1与双曲线y＝ 的一个交点为P(m，2).
(1)、求k的值；(2)、M(2，a)，N(n，b)是双曲线上的两点，直接写出当a＞b时，n的取值范围.20. 如图，在△ABC中，AB＝AC，∠BAC＝30°，将△ABC绕点A逆时针旋转α度(30＜α＜150)得到△AB′C′，B、C两点的对应点分别为点B′、C′，连接BC′，BC与AC、AB′相交于点E、F.
(1)、当α＝70时，∠ABC′＝°，∠ACB′＝°.(2)、求证：BC′∥CB′.21. 转转盘和摸球是等可能概率下的经典模型.
(1)、在一个不透明的口袋中，放入除颜色外其余都相同的4个小球，其中1个白球，3个黑球搅匀后，随机同时摸出2个球，求摸出两个都是黑球的概率(要求釆用树状图或列表法求解)；(2)、如图，转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次，求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解).22. 关于x的方程mx2﹣x﹣m+1＝0，有以下三个结论：①当m＝0时，方程只有一个实数解；
②当m≠0时，方程有两个不相等的实数解；
③无论m取何值，方程都有一个整数根.
(1)、请你判断，这三个结论中正确的有(填序号)(2)、证明(1)中你认为正确的结论.23. 如图，▱ABCD的对角线AC、BD相交于点M，点M在以AB为直径的⊙O上，AD与⊙O相交于点E，连接ME.
(1)、求证：ME＝MD；(2)、当∠DAB＝30°时，判断直线CD与⊙O的位置关系，并说明理由.24. 定义：在平面直角坐标系中，图形G上点P(x，y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”，记作Zp，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)、①点A(3，1)的“坐标差”为；②抛物线y＝﹣x2+5x的“特征值”为；
(2)、某二次函数y＝﹣x2+bx+c(c≠0)的“特征值”为﹣1，点B(m，0)与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等.①直接写出m＝；(用含c的式子表示)
②求此二次函数的表达式.
(3)、如图，在平面直角坐标系xOy中，点D(4，0)，以OD为直径作⊙M，直线y＝x+b与⊙M相交于点E、F.①比较点E、F的“坐标差”ZE、ZF的大小.
②请直接写出⊙M的“特征值”为.