浙江省宁波市象山县2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. “a是实数，a²≥0”这一事件是（）

A、必然事件 B、不确定事件 C、不可能事件 D、随机事件

查看试题解析
2. 正六边形的每个内角度数为（）

A、 $90^{\circ}$ B、 $108^{\circ}$ C、 $120^{\circ}$ D、 $150^{\circ}$

查看试题解析
3. 已知 $⊙ O$ 的面积为 $25 π$ ，圆心为原点O，则点 $P (5, 0)$ 与 $⊙ O$ 的位置关系是（）

A、在 $⊙ O$ 内 B、在 $⊙ O$ 上 C、在 $⊙ O$ 外 D、不能确定

查看试题解析
4. 如图，直线1_l//l₂//l₃ ，直线AC分别交 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 于点A，B，C，直线DF分别交 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 于点D，E， $F .$ 若 $\frac{A B}{B C} = \frac{2}{3}$ ，则 $\frac{D E}{D F}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{5}{2}$

查看试题解析
5. 已知圆的半径为3，扇形的圆心角为 $120^{\circ}$ ，则扇形的面积为（）

A、 $π$ B、 $2 π$ C、 $3 π$ D、 $4$

查看试题解析
6. 下列命题中，真命题为（）
$①$ 任意三点确定一个圆； $②$ 平分弦的直径垂直于弦； $③ 90^{\circ}$ 的圆周角所对的弦是直径； $④$ 同弧或等弧所对的圆周角相等.

A、 $② ③$ B、 $③ ④$ C、 $② ③ ④$ D、 $① ② ③ ④$

查看试题解析
7. 如图，矩形ABCD∽矩形DEFC，且面积比为4：1，则AE：ED的值为（）

A、4：1 B、3：1 C、2：1 D、3：2

查看试题解析
8. 已知 $(1, y_{1})$ ， $(2, y_{2})$ ， $(3, y_{3})$ 是抛物线 $y = - 2 x^{2} + 6 x + c$ 上的点，则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{1} = y_{2} < y_{3}$ D、 $y_{1} = y_{2} > y_{3}$

查看试题解析
9. 如图，AB为⊙O的直径，弦CD⊥AB，连结OD，AC，若∠CAO＝70°，则∠BOD的度数为（）

A、110° B、140° C、145° D、150°

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列结论中正确的是（）

A、 $a b c < 0$ B、 $2 a + b = 0$ C、 $4 a + 2 b + c = 0$ D、 $9 a + c < 3 b$

查看试题解析
11. 如图，网格中小正方形的边长都为1，点A，B，C在正方形的顶点处，则cos∠ACB的值为（）

A、 $\frac{2 \sqrt{34}}{17}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{85}}{17}$ D、 $\frac{7 \sqrt{85}}{85}$

查看试题解析
12. 如图，在 $Rt △ A O B$ 中， $∠ A B O = 90^{°}$ ， $∠ A O B = 30^{°}$ ， $A B=1$ ，扇形AOC的圆心角为 $60^{°}$ ，点D为 $\overset{⌢}{A C}$ 上一动点，P为BD的中点，当点D从点A运动至点C，则点P的运动路径长为（）

A、1 B、 $\frac{π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

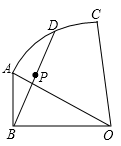查看试题解析

二、填空题

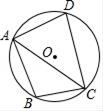
13. 若2a=3b，则a:b=.

查看试题解析
14. 某班共有6名学生干部，其中4名是男生，2名是女生，任意抽一名学生干部去参加一项活动，其中是女生的概率为．

查看试题解析
15. 若将抛物线 $y = - 2 {(x - 1)}^{2} + 1$ 向左平移3个单位，则所得图象的函数表达式为.

查看试题解析
16. 如图，四边形ABCD内接于⊙O，连结AC，若∠BAC＝35°，∠ACB＝40°，则∠ADC＝°.

查看试题解析
17. 如图，在矩形ABCD中， $A B = 8$ ， $B C = 6$ ，E为AD上一点，将 $△ B A E$ 绕点B顺时针旋转得到 $△ B A' E'$ ，当点 $A'$ ， $E'$ 分别落在BD，CD上时，则DE的长为.

查看试题解析
18. 如图，在 $⊙ O$ 中，弦BC，DE交于点P，延长BD，EC交于点A， $B C = 10$ ， $B P = 2 C P$ ，若 $\frac{B D}{A D} = \frac{2}{3}$ ，则DP的长为.

查看试题解析

三、解答题

19. 计算： $2 sin 60^{\circ} \cdot tan 45^{\circ} + {cos}^{2} 30^{\circ} - tan 60^{\circ}$

查看试题解析

20. 在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个，某学习小组进行摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再放回，下表是活动进行中的一组统计数据：

摸球的次数n	100	150	200	500	800	1000
摸到黑球的次数m	23	33	60	130	202	251
摸到黑球的频率 $\frac{m}{n}$	$0.23$	$0.22$	$0.30$	$0.26$	$0.2525$	$0.251$

(1)、当n很大时，估计从袋中摸出一个黑球的概率是；

(2)、试估算口袋中白球有个；

(3)、在

(2)

的条件下，若从中先换出一球，不放回，摇匀后再摸出一球，请用列表或树状图的方法求两次都摸到白球的概率.

查看试题解析

21. 如图，在数学活动课中，小明为了测量校园内旗杆AB的高度在地面上D处测得国旗顶部A点 $($ 即旗杆顶端 $)$ 和国旗底部C点的仰角分别为 $45^{\circ}$ 和 $42^{\circ}$ ，已知国旗的旗面高度 $A C = 1.28 m$ ，求旗杆AB高度 $. ($ 参考数据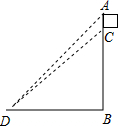： $sin 42^{\circ} \approx 0.67$ ， $cos 42^{\circ} \approx 0.74$ ， $tan 42^{\circ} \approx 0.90)$

查看试题解析
22. 中国的拱桥始建于东汉中后期，已有一千八百余年的历史，如图，一座拱桥在水面上方部分是AB，拱桥在水面上的跨度AB为8米，拱桥AB与水面的最大距离为3米.

(1)、用直尺和圆规作出AB所在圆的圆心O；

(2)、求拱桥AB所在圆的半径.

查看试题解析
23. 如图，在菱形ABCD中， $A B = 2$ ，点E为AB的中点， $∠ A D E = ∠ B E C$ .

(1)、求证： $△ A D E$ ∽ $△ E C D$ ；

(2)、求CE的长.

查看试题解析
24. 柑橘“红美人”汁多味美，入口即化，柔软无渣，经过试验，柑橘“红美人”单位面积的产量与单位面积的种植株数构成一种函数关系，每亩种植100株时，平均单株产量为20kg，每亩种植的株树每增加1株，平均单株产量减少0.1kg.

(1)、求平均单株产量y与每亩种植株数x的函数表达式；

(2)、今年柑橘“红美人”的市场价为40元/kg，并且每亩的种植成本为3万元，每亩种植多少株时，才能使得利润达到最大？最大为多少元？

查看试题解析
25. 定义：在平面直角坐标系xOy中，直线y＝a（x﹣m）+k称为抛物线y＝a（x﹣m）²+k的关联直线.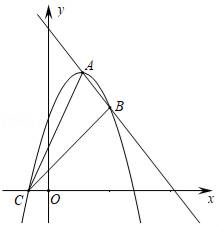

(1)、求抛物线y＝x²+6x﹣1的关联直线；

(2)、已知抛物线y＝ax²+bx+c与它的关联直线y＝2x+3都经过y轴上同一点，求这条抛物线的表达式；

(3)、如图，顶点在第一象限的抛物线y＝﹣a（x﹣1）²+4a与它的关联直线交于点A，B（点A在点B的左侧），与x轴负半轴交于点C，连结AC、BC.当△ABC为直角三角形时，求a的值.

查看试题解析
26. 如图，△ABC是⊙O的内接三角形，AB为⊙O直径，tan∠BAC= $\frac{3}{4}$ ，BC=3，点D为线段AC上一动点，过点D作AB的垂线交⊙O于点E，交AB于点F，连结BD，CF，并延长BD交⊙O于点H.

(1)、求⊙O的半径；

(2)、当DE经过圆心O时，求AD的长；

(3)、求证： $\frac{C F}{A F}$ = $\frac{B D}{A D}$ ；

(4)、求CF•DH的最大值.

查看试题解析