浙江省宁波市江北区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
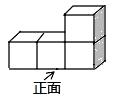
1. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、2. 从-5,-1,0, , 这五个数中随机抽取一个数,恰好为负整数的概率为( )A、 B、 C、 D、3. 如图所示的几何体是由4个相同的小正方体搭成的,它的主视图是( )
 A、
A、 B、
B、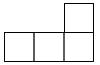 C、
C、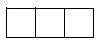 D、
D、 4. 在Rt△ABC中,∠C=90º, ,则 的值为( )A、 B、 C、 D5. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,若∠BAC=20°,则∠ADC的度数是( )
4. 在Rt△ABC中,∠C=90º, ,则 的值为( )A、 B、 C、 D5. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,若∠BAC=20°,则∠ADC的度数是( ) A、90° B、100° C、110° D、130°6. ⊙O与直线l有两个交点,且圆的半径为3,则圆心O到直线l的距离不可能是( )A、0 B、1 C、2 D、37. 将二次函数 的图像先向上平移3个单位,再向右平移4个单位所得图像的解析式为( )A、 B、 C、 D、8. 如图,在△ABC中,D,E分别在边AC与AB上,DE∥BC,BD、CE相交于点O, ,AE=1,则EB的长为( )
A、90° B、100° C、110° D、130°6. ⊙O与直线l有两个交点,且圆的半径为3,则圆心O到直线l的距离不可能是( )A、0 B、1 C、2 D、37. 将二次函数 的图像先向上平移3个单位,再向右平移4个单位所得图像的解析式为( )A、 B、 C、 D、8. 如图,在△ABC中,D,E分别在边AC与AB上,DE∥BC,BD、CE相交于点O, ,AE=1,则EB的长为( ) A、1 B、2 C、3 D、49. 已知二次函数 的函数值 与自变量 的部分对应值如下表,则下列判断中正确的是( )
A、1 B、2 C、3 D、49. 已知二次函数 的函数值 与自变量 的部分对应值如下表,则下列判断中正确的是( )…
-1
0
3
…
…
-5
1
-5
…
A、抛物线开口向上 B、抛物线的对称轴为直线 C、在 时, 随 增大而减小 D、抛物线与 轴只有一个交点10. 如图,将半径为3的圆形纸片,按下列顺序折叠两次.若折叠后的 和 都经过圆心 ,则图中阴影部分的面积是( ) A、 B、 C、 D、11. 如图,在 内(含边界)放置六个全等的正方形,这些正方形均有两个顶点在圆上,另两个顶点分别紧靠相邻正方形的顶点,则 的值为( )
A、 B、 C、 D、11. 如图,在 内(含边界)放置六个全等的正方形,这些正方形均有两个顶点在圆上,另两个顶点分别紧靠相邻正方形的顶点,则 的值为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,直线 不经过第四象限,且与 轴, 轴分别交于 两点,点 为 的中点,点 在线段 上,其坐标为 ,连结 , ,若 ,那么 的值为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,直线 不经过第四象限,且与 轴, 轴分别交于 两点,点 为 的中点,点 在线段 上,其坐标为 ,连结 , ,若 ,那么 的值为( ) A、 B、4 C、5 D、6
A、 B、4 C、5 D、6二、填空题
-
13. 做任意抛掷一只纸杯的重复实验,部分数据如下表
抛掷次数
50
100
500
800
1500
3000
5000
杯口朝上的频率
0.1
0.15
0.2
0.21
0.22
0.22
0.22
根据上表,可估计任意抛掷一只纸杯,杯口朝上的概率约为.
14. 已知圆锥的底面半径为 ,母线长为 ,则圆锥的侧面积为 .15. 如图是一块直角三角形木料, , , ,木工师傅要从中裁下一块圆形用料,则可裁圆形木料的最大半径为. 16. 若抛物线 的顶点在 轴的正半轴上,则 的值为.17. 如图,在 中,棱长为1的立方体的表面展开图有两条边分别在 , 上,有两个顶点在斜边 上,则 的面积为 .
16. 若抛物线 的顶点在 轴的正半轴上,则 的值为.17. 如图,在 中,棱长为1的立方体的表面展开图有两条边分别在 , 上,有两个顶点在斜边 上,则 的面积为 . 18. 如图,在平面直角坐标系中, , ,经过 两点的圆交 轴于点 ( 在 上方),则四边形 面积的最小值为.
18. 如图,在平面直角坐标系中, , ,经过 两点的圆交 轴于点 ( 在 上方),则四边形 面积的最小值为.
三、解答题
-
19. 计算: .20. 一个透明的布袋里装有2个红球, 个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为 .(1)、求 的值;(2)、先任意摸出1个球,记下颜色后不放回,搅匀,再摸出一个球,请利用画树状图或列表的方法求出连续两次都摸出红球的概率.21. 如图,“人字梯”放在水平地面上,梯子的两边相等(AB=AC),当梯子的一边AB与梯子两底端的连线BC的夹角α为60°时,BC的长为2米,若将α调整为65°时,求梯子顶端A上升的高度.(参考数据:sin65°≈0.91,cos65°=0.42,tan65°≈2.41, =1.73,结果精确到0.1m)
 22. 如图,在 的网格中,每个小正方形的边长均为1,点 在格点上,连结 ,请找一格点 ,使得 的三边之比恰好为 ,画出三个不同的三角形,并直接写出最长边的长度.(注意:全等三角形属于同一种情况)
22. 如图,在 的网格中,每个小正方形的边长均为1,点 在格点上,连结 ,请找一格点 ,使得 的三边之比恰好为 ,画出三个不同的三角形,并直接写出最长边的长度.(注意:全等三角形属于同一种情况) 23. 如图,已知二次函数 的图像经过点 , ,且对称轴为直线 ,一次函数 的图像经过 两点.
23. 如图,已知二次函数 的图像经过点 , ,且对称轴为直线 ,一次函数 的图像经过 两点. (1)、求二次函数的解析式;(2)、若点 关于抛物线的对称轴对称,根据图像直接写出满足 时 的取值范围.24. 如图, 是 的直径, 为 上一点, 与过点 的直线相互垂直,垂足为 ,且 平分 .
(1)、求二次函数的解析式;(2)、若点 关于抛物线的对称轴对称,根据图像直接写出满足 时 的取值范围.24. 如图, 是 的直径, 为 上一点, 与过点 的直线相互垂直,垂足为 ,且 平分 . (1)、求证: 是 的切线;(2)、若 , ,求 的半径.25. “垃圾分一分,明天美十分”.环保部门计划订制一批垃圾分类宣传海报,海报版面不小于300平方米,当宣传海报的版面为300平方米时,价格为80元/平方米.为了支持垃圾分类促进环保,广告公司给予以下优惠:宣传海报版面每增加1平方米,每平方米的价格减少0.2元,但不能低于50元/平方米.假设宣传海报的版面增加 平方米后,总费用为 元.(1)、求 关于 的函数表达式;(2)、订制宣传海报的版面为多少平方米时总费用最高?最高费用为多少元?(3)、环保部门希望总费用尽可能低,那么应该订制多少平方米的海报?26. 一个四边形被一条对角线分割成两个三角形,如果分割所得的两个三角形相似,我们就把这条对角线称为相似对角线.
(1)、求证: 是 的切线;(2)、若 , ,求 的半径.25. “垃圾分一分,明天美十分”.环保部门计划订制一批垃圾分类宣传海报,海报版面不小于300平方米,当宣传海报的版面为300平方米时,价格为80元/平方米.为了支持垃圾分类促进环保,广告公司给予以下优惠:宣传海报版面每增加1平方米,每平方米的价格减少0.2元,但不能低于50元/平方米.假设宣传海报的版面增加 平方米后,总费用为 元.(1)、求 关于 的函数表达式;(2)、订制宣传海报的版面为多少平方米时总费用最高?最高费用为多少元?(3)、环保部门希望总费用尽可能低,那么应该订制多少平方米的海报?26. 一个四边形被一条对角线分割成两个三角形,如果分割所得的两个三角形相似,我们就把这条对角线称为相似对角线.
 (1)、如图,正方形 的边长为4, 为 的中点,点 , 分别在边 和 上,且 ,线段 与 交于点 ,求证: 为四边形 的相似对角线;(2)、在四边形 中, 是四边形 的相似对角线, , , ,求 的长;(3)、如图,已知四边形 是圆 的内接四边形, , , ,点 是 的中点,点 是射线 上的动点,若 是四边形 的相似对角线,请直接写出线段 的长度(写出3个即可).
(1)、如图,正方形 的边长为4, 为 的中点,点 , 分别在边 和 上,且 ,线段 与 交于点 ,求证: 为四边形 的相似对角线;(2)、在四边形 中, 是四边形 的相似对角线, , , ,求 的长;(3)、如图,已知四边形 是圆 的内接四边形, , , ,点 是 的中点,点 是射线 上的动点,若 是四边形 的相似对角线,请直接写出线段 的长度(写出3个即可).