浙江省宁波市海曙区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 下列事件中,属于不可能事件的是( )A、明天会下雨 B、从只装有 个白球的袋子中摸出红球 C、抛一枚硬币正面朝上 D、在一个标准大气压下,加热到 水会沸腾2. 若 ,则 ( )A、 B、 C、 D、3. 二次函数y= 图像的对称轴是( )A、直线 B、直线 C、直线 D、直线4. 如图,在 中, , , ,则 的值是( )
 A、 B、 C、 D、5. 如图,圆 半径为 ,弓形高为 ,则弓形的弦 的长为( )
A、 B、 C、 D、5. 如图,圆 半径为 ,弓形高为 ,则弓形的弦 的长为( ) A、 B、 C、 D、6. 如图,在△ABC中,DE∥BC分别交AB,AC于点D,E,若 ,则下列说法不正确的是( )
A、 B、 C、 D、6. 如图,在△ABC中,DE∥BC分别交AB,AC于点D,E,若 ,则下列说法不正确的是( )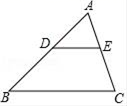 A、 B、 C、 D、7. 已知点A(1,y1),B(2 ,y2),C(4,y3)在二次函数y=x2﹣6x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y1<y3<y28. 如图, 为直径 的延长线上一点, 切⊙ 于点 ,若 ,则 ( )
A、 B、 C、 D、7. 已知点A(1,y1),B(2 ,y2),C(4,y3)在二次函数y=x2﹣6x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y1<y3<y28. 如图, 为直径 的延长线上一点, 切⊙ 于点 ,若 ,则 ( )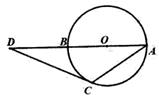 A、 B、 C、 D、9. 如图,三角形纸片 的周长为 , ,⊙ 是 的内切圆,玲玲用剪刀在⊙ 的左侧沿着与⊙ 相切的任意一条直线 剪下一个 ,则 的周长是( )
A、 B、 C、 D、9. 如图,三角形纸片 的周长为 , ,⊙ 是 的内切圆,玲玲用剪刀在⊙ 的左侧沿着与⊙ 相切的任意一条直线 剪下一个 ,则 的周长是( )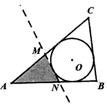 A、 B、 C、 D、根据 位置不同而变化10. 下列说法:①三点确定一个圆,②平分弦(不是直径)的直径垂直于弦,③相等的圆心角所对的弦相等,④三角形的内心到三边的距离相等,其中正确的有( )A、1个 B、2个 C、3个 D、4个11. 如图,已知⊙O的半径为5,弦AB=8,CD=6,则图中阴影部分面积为( )
A、 B、 C、 D、根据 位置不同而变化10. 下列说法:①三点确定一个圆,②平分弦(不是直径)的直径垂直于弦,③相等的圆心角所对的弦相等,④三角形的内心到三边的距离相等,其中正确的有( )A、1个 B、2个 C、3个 D、4个11. 如图,已知⊙O的半径为5,弦AB=8,CD=6,则图中阴影部分面积为( )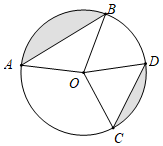 A、 π–24 B、9π C、 π–12 D、9π–612. 如图, 是半圆 的直径, 为弧 中点,点 、 分别在弦 、 上,且 .若设 , ,则 关于 的函数图象大致是( )
A、 π–24 B、9π C、 π–12 D、9π–612. 如图, 是半圆 的直径, 为弧 中点,点 、 分别在弦 、 上,且 .若设 , ,则 关于 的函数图象大致是( ) A、
A、 B、
B、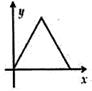 C、
C、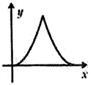 D、
D、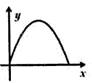
二、填空题
-
13. 口袋里装有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同,从中任意拿出一支笔芯,则笔芯为黑色的概率是.14. 已知点 是线段 的黄金分割点,且 ,若 ,则 长为.15. 已知扇形的弧长为 ,半径为 ,则此扇形的圆心角为度.16. 如图, 的两条中线 , 交于点 , 交 于点 ,若 ,则 .
 17. 如图抛物线 与直线 相交于点 、 ,与 轴交于点 ,若 为直角,则当 的时自变量 的取值范围是.
17. 如图抛物线 与直线 相交于点 、 ,与 轴交于点 ,若 为直角,则当 的时自变量 的取值范围是.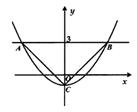 18. 如图, 是⊙ 的直径, , 为弧 中点,点 是⊙ 上一个动点,取弦 的中点 ,则 的最大值为.
18. 如图, 是⊙ 的直径, , 为弧 中点,点 是⊙ 上一个动点,取弦 的中点 ,则 的最大值为.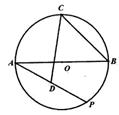
三、解答题
-
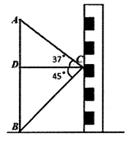
19. 计算:20. 如图,在数学活动课中,小敏为了测量校园内旗杆 的高度,站在教学楼上的 处测得旗杆底端 的俯角为 ,测得旗杆顶端 的仰角为 ,如旗杆与教学楼的水平距离 为 ,求旗杆的高度.
(参考数据: , )
 21. 2018年6月,某市全面推进生活垃圾分类工作.如图是某小区放置的垃圾桶,从左到右依次是红色:有害垃圾;蓝色:可回收垃圾;绿色:厨余垃圾;黑色:其他垃圾.
21. 2018年6月,某市全面推进生活垃圾分类工作.如图是某小区放置的垃圾桶,从左到右依次是红色:有害垃圾;蓝色:可回收垃圾;绿色:厨余垃圾;黑色:其他垃圾. (1)、居民A将一袋厨余垃圾随手放入一个垃圾桶,问他能正确投放垃圾的概率是.(2)、居民B手拎两袋垃圾,一袋是可回收垃圾,另一袋是有害垃圾。她先将可回收垃圾随手放入一个垃圾桶,然后把另一袋垃圾又随手放入其他垃圾桶。问:两袋垃圾都投放错误的概率?请画出树状图或列表说明理由.22. 如图,已知⊙ 的半径 垂直于弦 ,点 在 的延长线上, 平分
(1)、居民A将一袋厨余垃圾随手放入一个垃圾桶,问他能正确投放垃圾的概率是.(2)、居民B手拎两袋垃圾,一袋是可回收垃圾,另一袋是有害垃圾。她先将可回收垃圾随手放入一个垃圾桶,然后把另一袋垃圾又随手放入其他垃圾桶。问:两袋垃圾都投放错误的概率?请画出树状图或列表说明理由.22. 如图,已知⊙ 的半径 垂直于弦 ,点 在 的延长线上, 平分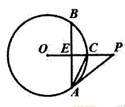 (1)、求证: 是⊙ 的切线;(2)、若 , ,求 .23. 如图是5◊5的正方形网格, 的三个顶点均在格点上.
(1)、求证: 是⊙ 的切线;(2)、若 , ,求 .23. 如图是5◊5的正方形网格, 的三个顶点均在格点上.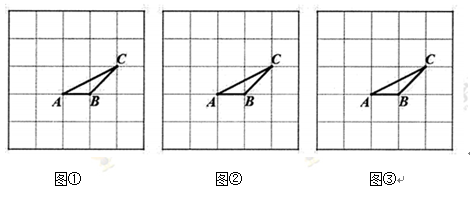 (1)、将 绕点 逆时针方向旋转 得到 ,在图①中作出 ;(2)、在图②中作一个与 相似且面积最大的格点 ;(3)、在图③中找出三个与点 、 、 在同一圆上的格点,并用 , , 标注.24. 如图,在斜坡上按水平距离间隔50米架设电缆,塔柱上固定电缆的位置 , 离塔柱底部的距离均为20米.若以点 为原点,以水平地面 所在的直线为 轴,建立如图所示的坐标系,已知斜坡 所在直线的解析式为 ,两端挂起的电缆下垂近似成二次项系数 为抛物线的形状.
(1)、将 绕点 逆时针方向旋转 得到 ,在图①中作出 ;(2)、在图②中作一个与 相似且面积最大的格点 ;(3)、在图③中找出三个与点 、 、 在同一圆上的格点,并用 , , 标注.24. 如图,在斜坡上按水平距离间隔50米架设电缆,塔柱上固定电缆的位置 , 离塔柱底部的距离均为20米.若以点 为原点,以水平地面 所在的直线为 轴,建立如图所示的坐标系,已知斜坡 所在直线的解析式为 ,两端挂起的电缆下垂近似成二次项系数 为抛物线的形状.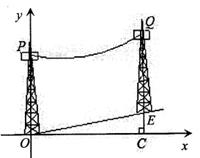 (1)、点 的坐标为,点 的坐标为;(2)、求电缆近似成的抛物线的解析式;(3)、小明说:在抛物线顶点处,下垂的电缆在竖直方向上与斜坡的距离最近。你是否认同?请计算说明。25. 定义:对角线互相垂直的圆内接四边形叫做圆的奇妙四边形.
(1)、点 的坐标为,点 的坐标为;(2)、求电缆近似成的抛物线的解析式;(3)、小明说:在抛物线顶点处,下垂的电缆在竖直方向上与斜坡的距离最近。你是否认同?请计算说明。25. 定义:对角线互相垂直的圆内接四边形叫做圆的奇妙四边形.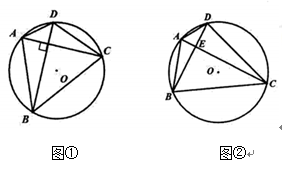 (1)、如图①,已知四边形 是⊙ 的奇妙四边形,若 , 则 ;(2)、如图②,已知四边形 内接于⊙ ,对角线交于点 ,若 ,
(1)、如图①,已知四边形 是⊙ 的奇妙四边形,若 , 则 ;(2)、如图②,已知四边形 内接于⊙ ,对角线交于点 ,若 ,①求证:四边形 是⊙ 的奇妙四边形;
②作 于 ,请猜想 与 之间的数量关系,并推理说明.
26. 如图,在平面直角坐标系中,已知 , , .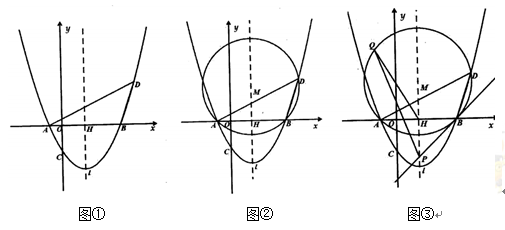 (1)、求过点 、 、 三点的抛物线解析式;(2)、在抛物线上取点 ,若点 的横坐标为10,求点 的坐标及 的度数;(3)、设抛物线对称轴 交 轴于点 , 的外接圆圆心为 (如图②)
(1)、求过点 、 、 三点的抛物线解析式;(2)、在抛物线上取点 ,若点 的横坐标为10,求点 的坐标及 的度数;(3)、设抛物线对称轴 交 轴于点 , 的外接圆圆心为 (如图②)①求点 的坐标及⊙ 的半径;
②过点 作⊙ 的切线交于 于点 (如图③),设 为⊙ 上一动点,则在点 运动过程中 的值是否变化?若不变,求出其值;若变化,请说明理由.