浙江省金华市东阳市2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 抛物线y＝﹣3x2+1的对称轴是（   ）
    A、直线x＝ 13 B、直线x＝﹣ 13 C、y轴 D、直线x＝3

    查看试题解析

  • 2. 如图所示的几何体的俯视图是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 3. 若关于x的方程x2+bx+1＝0有两个不相等的实数根，则b的值可以是（   ）
    A、0 B、1 C、2 D、3

    查看试题解析

  • 4. 如图，A，B是两座灯塔，在弓形AmB内有暗礁，游艇C在附近海面游弋，且∠AOB＝80°，要使游艇C不驶入暗礁区，则航行中应保持∠ACB（   ）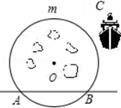

    A、小于40° B、大于40° C、小于80° D、大于80°

    查看试题解析

  • 5. 为了解某班学生一周的体育锻炼的时间，某综合实践活动小组对该班50名学生进行了统计如表:则这组数据中锻炼时间的众数是（   ）

    锻炼的时间（小时）

    7

    8

    9

    10

    学生人数（人）

    8

    16

    18

    8
    A、16人 B、8小时 C、9小时 D、18人

    查看试题解析

  • 6. 一张半径为6cm的扇形纸片卷成一个圆锥的侧面，要求圆锥底面圆的半径为4cm，那么这张扇形纸片的圆心角度数是（   ）
    A、150° B、240° C、200° D、180°

    查看试题解析

  • 7. 如图，在平行四边形ABCD中，AC与BD相交于点O，E是OD的中点，连接AE并延长交DC于点F，则DF：FC=（   ）

    A、1：4 B、1：3 C、1：2 D、1：1

    查看试题解析

  • 8. 在平面直角坐标系中，如果抛物线y＝3x2+3不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（   ）
    A、y＝3（x﹣2）2+5 B、y＝3（x+2）2+1 C、y＝3（x+2）2+5 D、y＝3（x﹣2）2+1

    查看试题解析

  • 9. 正多边形的内切圆与外接圆的周长之比为 3 ∶2，则这个正多边形为（ ）
    A、正十二边形 B、正六边形 C、正四边形 D、正三角形

    查看试题解析

  • 10. 如图，跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y＝ax2+bx+c（a≠0）.如图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（ ）

    A、10m B、20m C、15m D、22.5m

    查看试题解析

二、填空题

  • 11. 在函数y= x−1 的表达式中，自变量x的取值范围是.

    查看试题解析

  • 12. 如图，在△ABC中，EF∥BC，AE＝2BE，则△AEF与△ABC的面积比为.

    查看试题解析

  • 13. 已知A(1，y1)，B(2，y2)两点在双曲线y＝ m+3x 上，且y1＞y2 ， 则m的取值范围是.

    查看试题解析

  • 14. 如图，将矩形ABCD沿CE折叠，点B恰好落在边AD的F处，如果 ABBC=23 ，那么tan∠DCF的值是.

    查看试题解析

  • 15. 点A、C为半径是8的圆周上两动点，点B为 AC⌢ 的中点，以线段BA、BC为邻边作菱形ABCD，顶点D恰在该圆半径的中点上，则该菱形的边长为.

    查看试题解析

  • 16. 在平面直角坐标系xOy中，A（4，0），B（0，4），CD是△AOB的中位线.若将△COD绕点O旋转，得到△C′OD′，射线AC′与射线BD′的交点为P.

    (1)、∠APB的度数是°.
    (2)、在旋转过程中，记P点横坐标为m，则m的取值范围是.

    查看试题解析

三、解答题

  • 17. 计算: 2 sin45°﹣|﹣3|+（ 3 ﹣1）0+2﹣1.

    查看试题解析

  • 18. 如图，游客在点A处坐缆车出发，沿A﹣B﹣D的路线可至山顶D处，假设AB和BD都是直线段，且AB＝BD＝600m，α＝75°，β＝45°，求DE的长．

    （参考数据：sin75°≈0.97，cos75°≈0.26， 2 ≈1.41）

    查看试题解析

  • 19. 已知一次函数y＝x+4图象与反比例函数y＝ kx （k≠0）图象交于A（﹣1，a），B两点.

    (1)、求此反比例函数的表达式；
    (2)、若x+4≥ kx ，利用函数图象求x的取值范围.

    查看试题解析

  • 20. 今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：

    等级

    成绩（s）

    频数（人数）

    A

    90＜s≤100

    4

    B

    80＜s≤90

    x

    C

    70＜s≤80

    16

    D

    s≤70

    6

    根据以上信息，解答以下问题：

    (1)、表中的x=；
    (2)、扇形统计图中m= ， n= ， C等级对应的扇形的圆心角为度；
    (3)、该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1 ， a2表示）和两名女生（用b1 ， b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率.

    查看试题解析

  • 21. 如图，四边形ABCD内接于⊙O，∠BAD=90°，点E在BC的延长线上，且∠DEC=∠BAC.

    (1)、求证：DE是⊙O的切线；
    (2)、若AC∥DE，当AB=8，CE=2时，求AC的长.

    查看试题解析

  • 22. 某商品的进价为每件50元，售价为每件60元，每天可卖出190件；如果每件商品的售价每上涨1元，则每天少卖10件，设每件商品的售价上涨x元（x为正整数），每天的销售利润为y元．
    (1)、求y关于x的关系式；
    (2)、每件商品的售价定为多少元时，每天的利润恰为1980元？
    (3)、每件商品的售价定为多少元时，每天可获得最大利润？最大利润是多少元？

    查看试题解析

  • 23. 在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：

    如果矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形.点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形.例如，下图中的矩形A1B1C1D1 ， A2B2C2D2 ， AB3C3D3都是点A，B，C的覆盖矩形，其中矩形AB3C3D3是点A，B，C的最优覆盖矩形.

    (1)、已知A（﹣2，3），B（5，0），C（t，﹣2）.

    ①当t＝2时，点A，B，C的最优覆盖矩形的面积为；

    ②若点A，B，C的最优覆盖矩形的面积为40，求直线AC的表达式；

    (2)、已知点D（1，1）.E（m，n）是函数y＝ 4x （x＞0）的图象上一点，⊙P是点O，D，E的一个面积最小的最优覆盖矩形的外接圆，求出⊙P的半径r的取值范围.

    查看试题解析

  • 24. 如图，抛物线y＝ 13 x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B的坐标为（3，0），点C的坐标为（0，﹣5）.有一宽度为1，长度足够长的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线AC于点M和点N，交x轴于点E和点F.

    (1)、求抛物线的解析式及点A的坐标；
    (2)、当点M和N都在线段AC上时，连接MF，如果sin∠AMF＝ 1010 ，求点Q的坐标；
    (3)、在矩形的平移过程中，是否存在以点P，Q，M，N为顶点的四边形是平行四边形，若存在，求出点M的坐标；若不存在，请说明理由.

    查看试题解析