浙江省杭州市余杭区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 寒假即将来临，小明要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动，那么小明选择到甲社区参加实践活动的可能性为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{9}$

查看试题解析
2. 如图，已知⊙O中，半径OC垂直于弦AB，垂足为D，若OD=3，OA=5，则AB的长为（）

A、2 B、4 C、6 D、8

查看试题解析
3. 圆的面积公式S=πR²中，S与R之间的关系是（）

A、S是R的正比例函数 B、S是R的一次函数 C、S是R的二次函数 D、以上答案都不对

查看试题解析
4. 将二次函数 $y = x^{2}$ 的图象先向左平移1个单位，再向下平移2个单位，所得图象对应的函数表达式是（）

A、 $y = {(x + 1)}^{2} + 2$ B、 $y = {(x + 1)}^{2} - 2$ C、 $y = {(x - 1)}^{2} - 2$ D、 $y = {(x - 1)}^{2} + 2$

查看试题解析
5. 由 $\frac{x}{y} = \frac{2}{3}$ 不能推出的比例式是（）

A、 $\frac{x}{2} = \frac{y}{3}$ B、 $\frac{x + y}{y} = \frac{5}{3}$ C、 $\frac{x - y}{y} = \frac{1}{3}$ D、 $\frac{x + 2}{y + 3} = \frac{2}{3} (y \neq - 3)$

查看试题解析
6. 如图，点A，B，C都在⊙O上，若∠AOC=140°，则∠B的度数是（）

A、70° B、80° C、110° D、140°

查看试题解析
7. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的开口向上，与 $x$ 轴交点的横坐标分别为 $- 1$ 和3，则下列说法错误的是（）

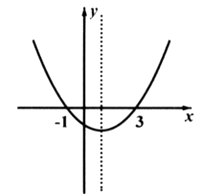A、对称轴是直线 $x = 1$ B、方程 $a x^{2} + b x + c = 0$ 的解是 $x_{1} = - 1$ ， $x_{2} = 3$ C、当 $- 1 < x < 3$ 时， $y < 0$ D、当 $x < 1$ ， $y$ 随 $x$ 的增大而增大

查看试题解析
8. 甲、乙两名同学在一次用频率去估计概率的实验中，绘出了某一结果出现的频率的折线图，则符合这一结果的实验可能是（）

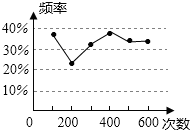A、掷一枚正六面体的骰子，出现1点的概率 B、抛一枚硬币，出现正面的概率 C、任意写一个整数，它能被2整除的概率 D、从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率

查看试题解析
9. 如图，在线段 $A B$ 上有一点 $C$ ，在 $A B$ 的同侧作等腰 $Δ A C D$ 和等腰 $Δ E C B$ ，且 $A C = A D$ ， $E C = E B$ ， $∠ D A C = ∠ C E B$ ，直线 $B D$ 与线段 $A E$ ，线段 $C E$ 分别交于点 $F ， G$ ，对于下列结论：① $Δ D C G$ ∽ $Δ B E G$ ；② $Δ A C E$ ∽ $Δ D C B$ ；③ $G F \cdot G B = G C \cdot G E$ ；④若 $∠ D A C = ∠ C E B = 90^{0}$ ，则 $2 A D^{2} = D F \cdot D G$ .其中正确的是（）

A、①②③④ B、①②③ C、①③④ D、①②

查看试题解析
10. 如图，在平面直角坐标系中，直线 $y = - x + 4$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，点 $C$ 是 $A B$ 的中点， $∠ E C D$ 绕点 $C$ 按顺时针旋转，且 $∠ E C D = 45^{0}$ ， $∠ E C D$ 的一边 $C E$ 交 $y$ 轴于点 $F$ ，开始时另一边 $C D$ 经过点 $O$ ，点 $G$ 坐标为 $(- 2 ， 0)$ ，当 $∠ E C D$ 旋转过程中，射线 $C D$ 与 $x$ 轴的交点由点 $O$ 到点 $G$ 的过程中，则经过点 $B ， C ， F$ 三点的圆的圆心所经过的路径长为（）

A、 $\frac{\sqrt{2}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $\frac{\sqrt{2}}{4}$

查看试题解析

二、填空题

11. 如果两个相似三角形的面积的比是4：9，那么它们对应的角平分线的比是．

查看试题解析
12. 如图，已知AB，CD是☉O的直径，弧AE=弧AC，∠AOE=32°，那么∠COE的度数为度.

查看试题解析
13. 如图，在平面直角坐标系中， $Δ D E F$ 是由 $Δ A B C$ 绕着某点旋转得到的，则这点的坐标是.

查看试题解析
14. 如图，已知点 $P$ 是 $Δ A B C$ 的重心，过 $P$ 作 $A B$ 的平行线 $D E$ ，分别交 $A C$ 于点 $D$ ，交 $B C$ 于点 $E$ ，作 $D F / / B C$ ，交 $A B$ 于点 $F$ ，若四边形 $B E D F$ 的面积为4，则 $Δ A B C$ 的面积为.

查看试题解析
15. 二次函数 $y = x^{2} - 4 x + 3$ 的图象与 $x$ 轴交于 $A ， B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ ，作直线 $l ： y = t (t > - 1)$ ，将直线 $l$ 下方的二次函数图象沿直线 $l$ 向上翻折，与其它剩余部分组成一个组合图象 $W$ ，若线段 $B C$ 与组合图象 $W$ 有两个交点，则 $t$ 的取值范围为.

查看试题解析

三、解答题

16. 已知 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$

(1)、求 $\frac{a + b + c}{b}$ 的值；

(2)、若 $2 a + b + 2 c = - 30$ ，求 $a, b, c$ 的值.

查看试题解析
17. 如图，已知二次函数 $y = x^{2} + b x + c$ 的图象经过点 $(- 1 ， 0)$ ， $(1 ， - 2)$ .

(1)、求 $b ， c$ 的值；

(2)、直接写出不等式 $x^{2} + b x + c < 0$ 的解.

查看试题解析
18. 周末，小马和小聪想用所学的数学知识测量图书馆前小河的宽.测量时，他们选择河对岸边的一棵大树，将其底部作为点 $A$ ，在他们所在的岸边选择了点 $B$ ，使得 $A B$ 与河岸垂直，并在 $B$ 点竖起标杆 $B C$ ，再在 $A B$ 的延长线上选择点 $D$ 竖起标杆 $D E$ ，使得点 $E$ 与点 $C$ ， $A$ 共线.
已知： $C B ⊥ A D$ ， $E D ⊥ A D$ ，测得 $B C = 1 m$ ， $D E = 1.35 m$ ， $B D = 7 m$ .测量示意图如图所示.请根据相关测量信息，求河宽 $A B$ .

查看试题解析
19. 在学习概率的课堂上，老师提出的问题：只有一张电影票，小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小丽和小芳都公平的方案.甲同学的方案：将红桃2、3、4、5四张牌背面向上，小丽先抽一张，小芳从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小丽看电影，否则小芳看电影.

(1)、甲同学的方案公平吗？请用列表或画树状图的方法说明；

(2)、乙同学将甲同学的方案修改为只用2、3、5、7四张牌，抽取方式及规则不变，乙的方案公平吗？并说明理由.

查看试题解析
20. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 上任意一点.

(1)、过 $A ， B ， D$ 三点作⊙ $O$ ，交线段 $A C$ 于点 $E$ （要求尺规作图，不写作法，但要保留作图痕迹）；

(2)、若弧DE=弧DB，求证： $A B$ 是⊙ $O$ 的直径.

查看试题解析
21. 元旦前夕，某企业接到一批粽子生产任务，约定这批粽子的出厂价为每只4元，按要求在20天内完成.为了按时完成任务，该企业招收了新工人，设新工人小丁第 $x$ 天生产的粽子数量为 $y$ 只， $y$ 与 $x$ 满足如下关系： $y = {\begin{array}{l} 34 x (0 \leq x \leq 6) \\ 20 x + 80 (6 < x \leq 20) \end{array}$

(1)、小丁第几天生产的粽子数量为280只？

(2)、如图，设第 $x$ 天生产的每只粽子的成本是 $p$ 元， $p$ 与 $x$ 之间的关系可用图中的函数图象来刻画.若小丁第 $x$ 天创造的利润为 $W$ 元，求 $W$ 与 $x$ 之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润=出厂价-成本）

查看试题解析
22. 如图，已知点 $B$ 的坐标是 $(- 2 ， 0)$ ，点 $C$ 的坐标是 $(8 ， 0)$ ，以线段 $B C$ 为直径作⊙ $A$ ，交 $y$ 轴的正半轴于点 $D$ ，过 $B$ 、 $C$ 、 $D$ 三点作抛物线.

(1)、求抛物线的解析式；

(2)、连结 $B D$ ， $C D$ ，点 $E$ 是 $B D$ 延长线上一点， $∠ C D E$ 的角平分线 $D F$ 交⊙ $A$ 于点 $F$ ，连结 $C F$ ，在直线 $B E$ 上找一点 $P$ ，使得 $Δ P F C$ 的周长最小，并求出此时点 $P$ 的坐标；

(3)、在（2）的条件下，抛物线上是否存在点 $G$ ，使得 $∠ G F C = ∠ D C F$ ，若存在，请直接写出点 $G$ 的坐标；若不存在，请说明理由.

查看试题解析