浙江省杭州市经济开发区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中，属于必然事件的是（）

A、三角形的外心到三边的距离相等 B、某射击运动员射击一次，命中靶心 C、任意画一个三角形，其内角和是 180° D、抛一枚硬币，落地后正面朝上

查看试题解析
2. tan45°的值为（）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
3. 如图，点B，C，D在⊙O上，若∠BCD＝130°，则∠BOD的度数是（）

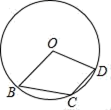A、50° B、60° C、80° D、100°

查看试题解析
4. 抛物线y=3（x﹣2）²+5的顶点坐标是（）

A、（﹣2，5） B、（﹣2，﹣5） C、（2，5） D、（2，﹣5）

查看试题解析
5. 点C为线段AB的黄金分割点，且AC＞BC，下列说法正确的有（）
①AC= $\frac{\sqrt{5} - 1}{2}$ AB，②AC= $\frac{3 - \sqrt{5}}{2}$ AB，③AB:AC=AC:BC，④AC≈0.618AB

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，△ABC中，AB=AC，AD是∠BAC的平分线.已知AB=10，tan∠B= $\frac{3}{4}$ ，则BC的长为（）

A、6 B、8 C、12 D、16

查看试题解析
7. 如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且∠AED＝∠B，再将下列四个选项中的一个作为条件，不一定能使得△ADE和△BDF相似的是（）

A、 $\frac{E A}{B D} = \frac{E D}{B F}$ B、 $\frac{E A}{B F} = \frac{E D}{B D}$ C、 $\frac{A D}{B D} = \frac{A E}{B F}$ D、 $\frac{B D}{B F} = \frac{B A}{B C}$

查看试题解析
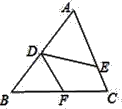8. 已知ABCD是一个以AD为直径的圆内接四边形，分别延长AB和DC，它们相交于P，若∠APD=60°，AB=5，PC=4，则⊙O的面积为（）

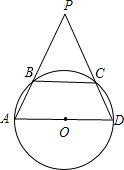A、25π B、16π C、15π D、13π

查看试题解析
9. 关于x的方程（x﹣3）（x﹣5）=m（m＞0）有两个实数根α，β（α＜β），则下列不符合题意的是（）

A、3＜α＜β＜5 B、3＜α＜5＜β C、α＜2＜β＜5 D、α＜3且β＞5

查看试题解析
10. 在Rt△ABC中，∠C＝90°，AB＝4，AC＝1，则cosB的值为（）

A、 $\frac{\sqrt{15}}{4}$ B、 $\frac{1}{4}$ C、 $\frac{\sqrt{15}}{15}$ D、 $\frac{4 \sqrt{17}}{17}$

查看试题解析

二、填空题

11. 袋中装有6个黑球和n个白球，经过若干次试验，发现“若从袋中任摸出一个球，恰是黑球的概率为 $\frac{3}{4}$ ，则这个袋中白球大约有个．

查看试题解析
12. 若二次函数 $y = a x^{2} + 2 a x - 3$ 的图象与x轴的一个交点是（2，0），则与x轴的另一个交点坐标是．

查看试题解析
13. 某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示，已知AB=16m，半径OA=10m，则中间柱CD的高度为m.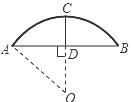

查看试题解析
14. 某轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，又继续航行7海里后，在B处测得小岛P的方位是北偏东60°，则此时轮船与小岛P的距离BP=海里．

查看试题解析
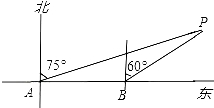15. 如图，在△ABC中，∠A=60°，⊙O为△ABC的外接圆.如果BC=2 $\sqrt{3}$ ，那么⊙O的半径为.

查看试题解析
16. 如图所示，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE＝1：3，则S△BDE：S四边形DECA的值为.

查看试题解析

三、解答题

17. 经过校园某路口的行人，可能左转，也可能直行或右转．假设这三种可能性相同，现有小明和小亮两人经过该路口，请用列表法或画树状图法，求两人之中至少有一人直行的概率．

查看试题解析
18. 如图，△ABC中，点D在边AB上，满足∠ACD=∠ABC，若AC= $\sqrt{3}$ ，AD=1，求DB的长.

查看试题解析
19. 如图，已知四边形ABCD内接于圆O，∠A=105°，BD=CD.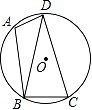

(1)、求∠DBC的度数；

(2)、若⊙O的半径为3，求 $\overset{⌢}{B C}$ 的长.

查看试题解析
20. 如图，一条公路的两侧互相平行，某课外兴趣小组在公路一侧AE的点A处测得公路对面的点C与AE的夹角∠CAE=30°，沿着AE方向前进15米到点B处测得∠CBE=45°，求公路的宽度.（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.73）

查看试题解析
21. 绿色生态农场生产并销售某种有机产品，假设生产出的产品能全部售出.如图，线段EF、折线ABCD分别表示该有机产品每千克的销售价y₁（元）、生产成本y₂（元）与产量x（kg）之间的函数关系.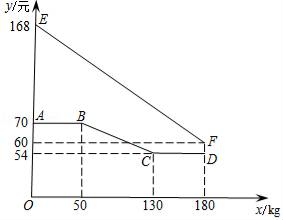

(1)、求该产品销售价y₁（元）与产量x（kg）之间的函数关系式；

(2)、直接写出生产成本y₂（元）与产量x（kg）之间的函数关系式；

(3)、当产量为多少时，这种产品获得的利润最大？最大利润为多少？

查看试题解析
22. 二次函数y=ax²+2x﹣1与直线y=2x﹣3交于点P（1，b）.

(1)、求出此二次函数的解析式；

(2)、求此二次函数的顶点坐标，并指出x取何值时，该函数的y随x的增大而减小.

查看试题解析
23. 阅读材料：小胖同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1，在“手拉手”图形中，小胖发现若∠BAC＝∠DAE，AB＝AC，AD＝AE，则BD＝CE.

(1)、在图1中证明小胖的发现；
借助小胖同学总结规律，构造“手拉手”图形来解答下面的问题：

(2)、如图2，AB＝BC，∠ABC＝∠BDC＝60°，求证：AD+CD＝BD；

(3)、如图3，在△ABC中，AB＝AC，∠BAC＝m°，点E为△ABC外一点，点D为BC中点，∠EBC＝∠ACF，ED⊥FD，求∠EAF的度数（用含有m的式子表示）.

查看试题解析