浙江宁波市慈溪2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,将点 绕坐标原点 顺时针旋转 ,所得到的对应点 的坐标为( )A、 B、 C、 D、2. 下列四条圆弧与直角三角板的位置关系中,可判断其中的圆弧为半圆的是( )A、
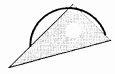 B、
B、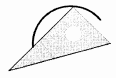 C、
C、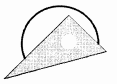 D、
D、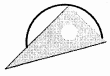 3. 下列事件是随机事件的是( )A、在标准大气压下,水加热到 时沸腾 B、小明购买1张彩票,中奖 C、在一个装有红球和黄球的袋中,摸出蓝球 D、一名运动员跳高的最好成绩是10.1米4. 如图, 是正六边形 的外接圆, 是弧 上一点,则 的度数是( )
3. 下列事件是随机事件的是( )A、在标准大气压下,水加热到 时沸腾 B、小明购买1张彩票,中奖 C、在一个装有红球和黄球的袋中,摸出蓝球 D、一名运动员跳高的最好成绩是10.1米4. 如图, 是正六边形 的外接圆, 是弧 上一点,则 的度数是( )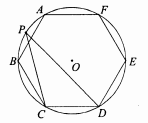 A、 B、 C、 D、5. 由抛物线y=x2平移得到抛物线y=(x+2)2 , 下列平移方法可行的是( )A、向上平移2个单位长度 B、向下平移2个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度6. 下列命题:①三点确定一个圆;②三角形的外心到三边的距离相等;③相等的圆周角所对的弧相等;④平分弦的直径垂直于弦.其中假命题的个数是( )A、1 B、2 C、3 D、47. 关于抛物线 ,下列说法错误的是( )A、顶点坐标为 B、对称轴是直线 C、若 ,则 随 的增大而增大 D、当 时,8. 如图, , , 是正方形网格中的格点(小正方形的顶点),则 的值为( )
A、 B、 C、 D、5. 由抛物线y=x2平移得到抛物线y=(x+2)2 , 下列平移方法可行的是( )A、向上平移2个单位长度 B、向下平移2个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度6. 下列命题:①三点确定一个圆;②三角形的外心到三边的距离相等;③相等的圆周角所对的弧相等;④平分弦的直径垂直于弦.其中假命题的个数是( )A、1 B、2 C、3 D、47. 关于抛物线 ,下列说法错误的是( )A、顶点坐标为 B、对称轴是直线 C、若 ,则 随 的增大而增大 D、当 时,8. 如图, , , 是正方形网格中的格点(小正方形的顶点),则 的值为( ) A、 B、 C、 D、9. 如图,在 中, , 分别是边 , 上的点, , ,下列结论中错误的是( )
A、 B、 C、 D、9. 如图,在 中, , 分别是边 , 上的点, , ,下列结论中错误的是( ) A、 B、 C、 D、10. 如图,在 中, , ,分别以点 和点 为圆心,以 的长为半径画弧交 于 , 两点,则阴影部分的面积是( )
A、 B、 C、 D、10. 如图,在 中, , ,分别以点 和点 为圆心,以 的长为半径画弧交 于 , 两点,则阴影部分的面积是( )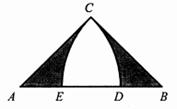 A、 B、 C、 D、11. 在平面直角坐标系中,对于点 和 ,给出如下定义:若 ,则称点 为点 的“亲密点”.例如:点 的“亲密点”为点 ,点 的“亲密点”为点 .若点 在函数 的图象上.则其“亲密点” 的纵坐标 关于 的函数图象大致正确的是( )A、
A、 B、 C、 D、11. 在平面直角坐标系中,对于点 和 ,给出如下定义:若 ,则称点 为点 的“亲密点”.例如:点 的“亲密点”为点 ,点 的“亲密点”为点 .若点 在函数 的图象上.则其“亲密点” 的纵坐标 关于 的函数图象大致正确的是( )A、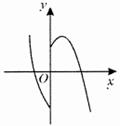 B、
B、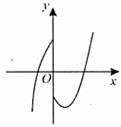 C、
C、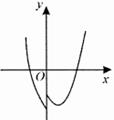 D、
D、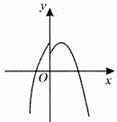 12. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,过 , , 三点作圆,点 在第一象限部分的圆上运动,连结 ,过点 作 的垂线交 的延长线于点 ,下列说法:① ;② ;③ 的最大值为10.其中正确的是( )
12. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,过 , , 三点作圆,点 在第一象限部分的圆上运动,连结 ,过点 作 的垂线交 的延长线于点 ,下列说法:① ;② ;③ 的最大值为10.其中正确的是( )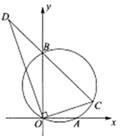 A、①② B、②③ C、①③ D、①②③
A、①② B、②③ C、①③ D、①②③二、填空题
-
13. 已知 是锐角,且 ,则 的度数是º.14. 如图,显示的是用计算机模拟随机投掷一枚图钉的某次试验的结果.小明根据试验结果推断:随着重复试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,就可以估计“钉尖向上”的概率是0.618.你认为小明的推断是(填写“正确”或“错误”)的.
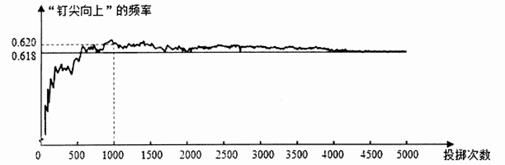 15. 矩形的两边长分别为 和6( ),把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则 .
15. 矩形的两边长分别为 和6( ),把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则 .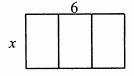 16. 如图,在 中, , , ,点 是 的重心,连接 并延长交 于点 ,则 .
16. 如图,在 中, , , ,点 是 的重心,连接 并延长交 于点 ,则 .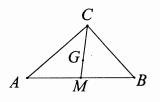 17. 如图, , , 是 上三点,若 , 的半径为2,则劣弧 的长为.
17. 如图, , , 是 上三点,若 , 的半径为2,则劣弧 的长为.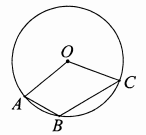 18. 如图,抛物线 与 轴交于 , 两点(点 在点 的左边)与 轴交于点 ,连接 ,过点 作直线 的平行线交抛物线于另一点 ,交 轴于点 ,则 的值为.
18. 如图,抛物线 与 轴交于 , 两点(点 在点 的左边)与 轴交于点 ,连接 ,过点 作直线 的平行线交抛物线于另一点 ,交 轴于点 ,则 的值为.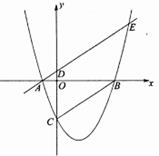
三、解答题
-
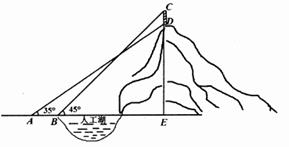
19.(1)、计算: .(2)、已知 ,求 与 的比.20. 在三个完全相同的小球上分别写上-2,-1,2三个数字,然后装入一个不透明的布袋内搅匀,从布袋中取出一个球,记下小球上的数字为 ,放回袋中再搅匀,然后再从袋中取出一个小球,记下小球上的数字为 ,组成一对数 .(1)、请用列表或画树状图的方法,表示出数对 的所有可能的结果;(2)、求直线 不经过第一象限的概率.21. 某公园的人工湖边上有一座山,山顶上有一直竖的建筑物 ,高为10米.某校数学兴趣小组的同学为了测量山的高度 ,在公园找了一水平地面,在 处测得建筑物点 (即山顶)的仰角为 ,沿水平方向前进20米到达 点,测得建筑物顶部 点的仰角为 ,求山的高度 .(结果精确到1米,参考数据: , , )
 22. 如图,已知A、B、C是⊙O上三点,其中 ,过点B画BD⊥OC于点D.
22. 如图,已知A、B、C是⊙O上三点,其中 ,过点B画BD⊥OC于点D.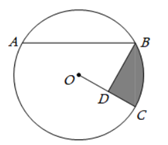 (1)、求证:AB=2BD;(2)、若AB= ,CD=1,求图中阴影部分的面积.23. 如图,已知 是 斜边 上的中线,过点 作 的平行线,过点 作 的垂线,两线相交于点 .
(1)、求证:AB=2BD;(2)、若AB= ,CD=1,求图中阴影部分的面积.23. 如图,已知 是 斜边 上的中线,过点 作 的平行线,过点 作 的垂线,两线相交于点 .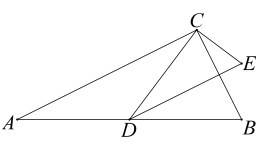 (1)、求证: ;(2)、若 , ,求 的面积.24. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润 与投资金额 成正比例关系,如图1所示;种植花卉的利润 与投资金额 成二次函数关系,如图2所示.(注:利润与投资金额的单位均为万元)
(1)、求证: ;(2)、若 , ,求 的面积.24. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润 与投资金额 成正比例关系,如图1所示;种植花卉的利润 与投资金额 成二次函数关系,如图2所示.(注:利润与投资金额的单位均为万元)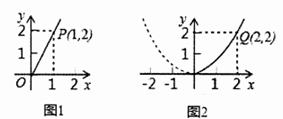 (1)、分别求出利润 与 关于投资金额 的函数关系;(2)、如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉的金额是 万元,求这位专业户能获取的最大总利润是多少万元?25. 四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.
(1)、分别求出利润 与 关于投资金额 的函数关系;(2)、如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉的金额是 万元,求这位专业户能获取的最大总利润是多少万元?25. 四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.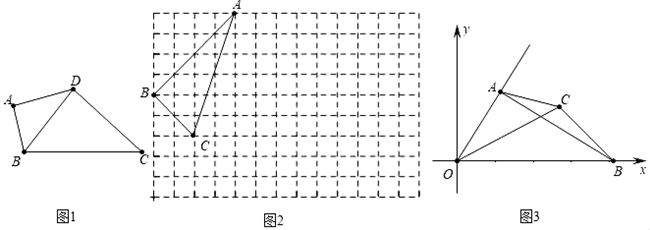 (1)、如图1,在四边形ABCD中,∠ABC=100°,∠ADC=130°,BD≠BC,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;(2)、如图2,已知格点△ABC,请你在正方形网格中画出所有的格点四边形ABCD,使四边形ABCD是以AC为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)(3)、如图3,四边形AOBC中,点A在射线OP: (x≥0)上,点B在x轴正半轴上,对角线OC平分∠AOB,连接AB.若OC是四边形AOBC的“相似对角线”,S△AOB=6 ,求点C的坐标.26. 如图1,抛物线 交 轴于点 和点 ,交 轴于点 ,一次函数 的图象经过点 , ,点 是抛物线上第二象限内一点.
(1)、如图1,在四边形ABCD中,∠ABC=100°,∠ADC=130°,BD≠BC,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;(2)、如图2,已知格点△ABC,请你在正方形网格中画出所有的格点四边形ABCD,使四边形ABCD是以AC为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)(3)、如图3,四边形AOBC中,点A在射线OP: (x≥0)上,点B在x轴正半轴上,对角线OC平分∠AOB,连接AB.若OC是四边形AOBC的“相似对角线”,S△AOB=6 ,求点C的坐标.26. 如图1,抛物线 交 轴于点 和点 ,交 轴于点 ,一次函数 的图象经过点 , ,点 是抛物线上第二象限内一点.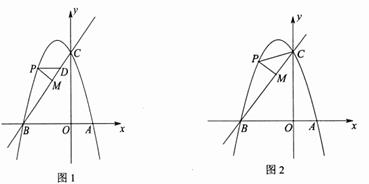 (1)、求二次函数和一次函数的表达式;(2)、过点 作 轴的平行线交 于点 ,作 的垂线 交 于点 ,设点 的横坐标为 , 的周长为 .
(1)、求二次函数和一次函数的表达式;(2)、过点 作 轴的平行线交 于点 ,作 的垂线 交 于点 ,设点 的横坐标为 , 的周长为 .①求 关于 的函数表达式;
②求 的周长的最大值及此时点 的坐标;
(3)、如图2,连接 ,是否存在点 ,使得以 , , 为顶点的三角形与 相似?若存在,直接写出点 的横坐标;若不存在,请说明理由.