广西钦州市钦州港区2019届九年级上学期数学期末考试试卷
试卷更新日期：2019-08-05 类型：期末考试
一、单选题
-
1. 若一元二次方程x2﹣x﹣6=0的两根为x1 ， x2 ， 则x1+x2的值为（ ）A、1 B、﹣1 C、0 D、﹣62. 用配方法方程x2+6x﹣5=0时，变形正确的方程为（ ）A、（x+3）2=14 B、（x﹣3）2=14 C、（x+6）2=4 D、（x﹣6）2=43. 一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球，从中随机摸出一个，摸到黄球的概率是( )
A、 B、 C、 D、4. 下列方程中，有两个不相等的实数根的是（ ）A、x2﹣3x+8=0 B、x2+5x=10 C、3x2﹣x+2=0 D、x2﹣2x=﹣15. 如图，△ABC内接于⊙O，若∠OAB=28°，则∠C的大小为（ ）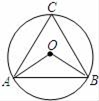
A、28° B、26° C、60° D、62°6. 如图，直线AB与⊙O相切于点A，⊙O的半径为1，若∠OBA=30°，则OB长为（ ）
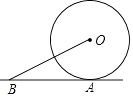A、1 B、2 C、 D、27. 如图，在正方形网格中，将三角形ABC绕点A旋转后得到三角形ADE，则下列旋转方式中，符合题意的是（ ）
A、顺时针旋转90° B、逆时针旋转90° C、顺时针旋转45° D、逆时针旋转45°8. 下列关于抛物线y＝3（x﹣1）2+1的说法，正确的是（ ）A、开口向下 B、对称轴是x＝﹣1 C、顶点坐标是（﹣1，1） D、有最小值y＝19. 已知反比函数 ，下列结论中不正确的是（ ）A、图象必经过点 B、图象位于第二、四象限 C、若 则 D、在每一个象限内， 随 值的增大而减小10. 将1，2，3三个数字随机生成的点的坐标，列成下表.如果每个点出现的可能性相等，那么从中任意取一点，则这个点在函数y=x图象上的概率是（ ）（1，1）
（1，2）
（1，3）
（2，1）
（2，2）
（2，3）
（3，1）
（3，2）
（3，3）
A、0.3 B、0.5 C、 D、11. 已知函数y= 的图象如图，当x≥﹣1时，y的取值范围是（ ）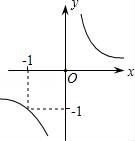
A、y＜﹣1 B、y≤﹣1 C、y≤﹣1或y＞0 D、y＜﹣1或y≥012. 抛物线图象如图所示，根据图象，抛物线的解析式可能是（ ）
A、y=x2﹣2x+3 B、y=﹣x2﹣2x+3 C、y=﹣x2+2x+3 D、y=﹣x2+2x﹣3二、填空题
-
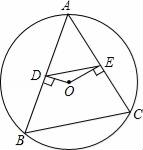
13. 若关于x的方程3x2﹣2x+m=0的一个根为﹣1，则m的值为.14. 已知反比例函数y＝ ，x＞0时，y0，这部分图象在第象限，y随着x值的增大而.15. 将抛物线y=﹣3x2的图象向右平移2个单位，再向下平移1个单位，所得到的图象对应的抛物线的解析式是.16. 如图，△ABC为⊙O的内接三角形，O为圆心，OD⊥AB于点D，OE⊥AC于点E，若DE=2，则BC=.
17. 如图△ABC中，∠A=30°，∠C=90°，作△ABC的外接圆.若弧AB的长为12cm，那么弧AC的长是.
18. 如图，有6张扑克牌，从中任意抽取两张，点数和是偶数的概率是.
三、解答题
-
19.(1)、解下列方程：
①x2﹣6x﹣16=0
②2x2﹣5x+3=0
(2)、关于x的一元二次方程kx2+（k﹣1）x﹣3=0有一个根为3，求k的值及另一个根.20. 甲口袋有2个相同的小球，它们分别写有数字1和2，乙口袋中装有3个相同的小球，它们分别写有数字3、4、5，从这两个口袋中各随机地取出1个球.(1)、用“树状图法”或“列表法”表示所有可能出现的结果；(2)、取出的两个小球上所写数字之和是偶数的概率是多少？21. 如图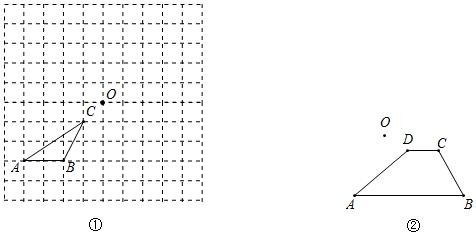
①在图①中画出△ABC 绕点O顺时针旋转90°后的图形；
②在图②中画出四边形ABCD关于点O对称的图形.
22. 为进一步发展基础教育，自2014年以来，某县加大了教育经费的投入，2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。(1)、求这两年该县投入教育经费的年平均增长率；(2)、若该县教育经费的投入还将保持相同的年平均增长率，请你预算2017年该县投入教育经费多少万元。23. 已知抛物线y=ax2+c与x轴交于A、B两点，顶点为C，点P在抛物线上，且P（1，﹣3），B（4，0）
(1)、求点A的坐标(2)、求该抛物线的解析式；(3)、直接写出该抛物线的顶点C的坐标.
