广西柳州市柳南区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列平面图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
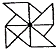2. 下列事件是必然事件的是（）

A、抛掷一枚硬币四次，有两次正面朝上 B、打开电视频道，正在播放《今日在线》 C、射击运动员射击一次，命中十环 D、方程x²-x=0必有实数根

查看试题解析
3. 如图，直线a，b被直线c所截，下列条件能判断a∥b的是（）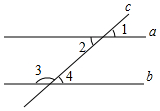

A、∠1=∠2 B、∠1=∠4 C、∠3+∠4=180° D、∠2=30°，∠4=35°

查看试题解析
4. 习近平总书记提出了未来5年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（）

A、1.17×10⁶ B、1.17×10⁷ C、1.17×10⁸ D、11.7×10⁶

查看试题解析
5. 关于x的方程（m﹣1）x²+2mx﹣3＝0是一元二次方程，则m的取值是（）

A、任意实数 B、m≠1 C、m≠﹣1 D、m＞1

查看试题解析
6. 如图，A，B，C三点在⊙O上，∠AOB＝80º，则∠ACB的大小（）

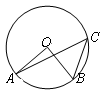A、40º B、60º C、80º D、100º

查看试题解析
7. 对于二次函数y=（x-1）²+2的图象，下列说法正确的是（　　）

A、开口向下 B、对称轴是x=-1 C、顶点坐标是（1，2） D、与x轴有两个交点

查看试题解析
8. 下列计算正确的是（）

A、 $2 x - x = 1$ B、 $x (- x) = - 2 x$ C、 ${(x^{2})}^{3} = x^{6}$ D、 $x^{2} + x = 2$

查看试题解析
9. 如图，点D在△ABC边BC的延长线上，CE平分∠ACD，∠A＝80°，∠B＝40°，则∠ACE的大小是（）

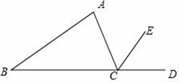A、30° B、40° C、50° D、60°

查看试题解析
10. 如图，△OAB绕点O逆时针旋转80°到△OCD的位置，已知∠AOB=45°，则∠AOD等于（）

A、55° B、45° C、40° D、35°

查看试题解析
11. Rt ABC中，∠C＝90°，AC＝8cm，BC＝6cm，以点C为圆心，5cm为半径的圆与直线AB的位置关系是（）

A、相切 B、相交 C、相离 D、无法确定

查看试题解析
12. 如图，是二次函数y＝ax²+bx+c的图象，①abc＞0；②a+b+c＜0；③4a﹣2b+c＜0；④4ac﹣b²＜0，其中正确结论的序号是（）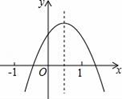

A、①②③ B、①③ C、②④ D、③④

查看试题解析

二、填空题

13. 点P（4，﹣3），则点P关于原点的对称点P′坐标是.

查看试题解析
14. 某小组5名同学的身高（单位：cm）分别为：147，156，151，159，152，则这组数据的中位数是cm.

查看试题解析
15. 分式方程 $\frac{x - 2}{x} = \frac{1}{2}$ 的解为 .

查看试题解析
16. 已知圆锥的底面半径为2cm，母线长是4cm，则圆锥的侧面积是cm²（结果保留π）．

查看试题解析
17. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝6，BE＝1，则弦CD的长是.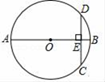

查看试题解析
18. 如图是在正方形网格中按规律填成的阴影，根据此规律，若第n个图中阴影部分小正方形的个数为440个，则n的值是.

查看试题解析

三、解答题

19. 解一元二次方程 $x^{2} + 2 x - 3 = 0$

查看试题解析
20. 钦州市某中学为了解本校学生阅读教育、科技、体育、艺术四类课外书的喜爱情况，随机抽取了部分学生进行问卷调查，在此次调查中，甲、乙两班分别有2人特别喜爱阅读科技书报，若从这4人中随机抽取2人去参加科普比赛活动，请用列表法或画树状图的方法，求所抽取的2人来自不同班级的概率．

查看试题解析
21. 如图，点A、D、C、F在同一条直线上，AD=CF，AB=DE，BC=EF.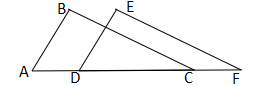

(1)、求证：ΔABC≌△DEF；

(2)、若∠A=55°，∠B=88°，求∠F的度数.

查看试题解析
22. 如图，△ABC各顶点的坐标分别是A（﹣2，﹣4），B（0，﹣4），C（1，﹣1）.

(1)、①在图中画出△ABC向左平移3个单位后的△A₁B₁C₁；
②在图中画出△ABC绕原点O逆时针旋转90°后的△A₂B₂C₂；

(2)、在（1）②的条件下，AC边扫过的面积是.

查看试题解析
23. 如图，正比例函数y＝2x的图象与一次函数y＝kx+b的图象交于点A（m，2），一次函数图象经过点B（﹣2，﹣1），与y轴的交点为C，与x轴的交点为D.

(1)、求一次函数解析式；

(2)、求C点的坐标；

(3)、求△AOD的面积.

查看试题解析
24. 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱.

(1)、求平均每天销售量 $y$ 箱与销售价 $x$ 元/箱之间的函数关系式.

(2)、求该批发商平均每天的销售利润w（元）与销售价 $x$ （元/箱）之间的函数关系式.

(3)、当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？

查看试题解析
25. 如图，⊙O的直径AB＝6，AM，BN是⊙O的两条切线，点D是AM上一点，连接OD，作BE∥OD交⊙O于点E，连接DE并延长交BN于点.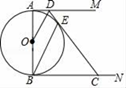

(1)、求证：DC是⊙O的切线；

(2)、设AD＝x，BC＝y.求y与x的函数关系式（不要求写出自变量的取值范围）

(3)、若AD＝1，连接AE并延长交BC于F，求EF的长.

查看试题解析
26. 如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．

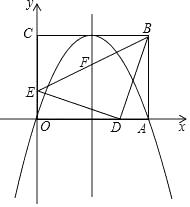(1)、求抛物线的解析式；

(2)、猜想△EDB的形状并加以证明；

(3)、点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

查看试题解析