浙江省宁波市鄞州区七校2018-2019学年八年级上学期数学10月联考试卷
试卷更新日期：2019-08-05 类型：月考试卷
一、单选题
-
1. 下列图案是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列说法错误的是（ ）A、全等三角形的面积相等 B、全等三角形的周长相等 C、面积相等的三角形全等 D、面积不等的三角形不全等3. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
A、10 B、7 C、5 D、44. 若一个三角形的三条高线交点恰好是此三角形的一个顶点，则此三角形一定是（ ）A、等腰三角形 B、等边三角形 C、等腰直角三角形 D、直角三角形5. 如图，在Rt△ABC中，∠C=90°，直线DE是斜边AB的垂直平分线交AC于D ． 若AC=8，BC=6，则△DBC的周长为（ ）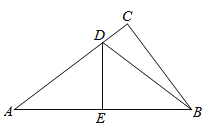
A、12 B、14 C、16 D、无法计算6. 下列命题中，正确的有（ ）①Rt△ABC中，已知两边长分别为3和4，则第三边长为5；
②有一个内角等于其他两个内角和的三角形是直角三角形；
③三角形的三边分别为a，b，C，若a2+c2=b2 ， 那么∠C=90°；
④若△ABC中，∠A：∠B：∠C=1：5：6，则△ABC是直角三角形．
A、1个 B、2个 C、3个 D、4个7. 如图△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D交AC于点E，那么下列结论中正确的是（ ）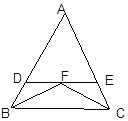
①△BDF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF=CF
A、①②③④ B、①②③ C、①② D、①8. 如图，把△ 沿 对折，叠合后的图形如图所示.若 ， ，则∠2的度数为（ ）
A、24° B、35° C、30° D、25°9. 如图，一个正方形被分成三十六个面积均为1的小正方形，点A与点B在两个格点上，问在格点上是否存在一个点，使△ABC的面积为2，这样的点有（ ）个.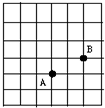
A、7个 B、6个 C、5个 D、4个二、填空题
-
10. 一个等腰三角形的底边长为 5，一腰上中线把其周长分成的两部分的差为 3，则这个等腰三角形的腰长为
11. 如图，已知AC=DB，要使△ABC≌△DCB，则需要补充的条件为.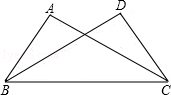
12. 已知一个等腰三角形两边分别为4和6，那么这个等腰三角形的周长为 ．
13. 学校有一长方形花圃，有极少数人为了避开拐角而走“捷径”.在花圃内走出了一条“路”，其实他们仅仅少走了米，但是却踩伤花草.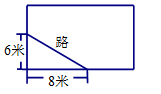
14. 如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG=CD，DF=DE，则∠EFD=°.
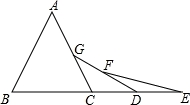15. 两边长分别为5，12的直角三角形，其斜边上的中线长为.16. 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于度.
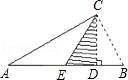17. 如图，在△ABC中，分别以AC、BC为边作等边三角形ACD和等边三角形BCE，连接AE、BD交于点O，则∠AOB的度数为。
18. 如图，在Rt△ABC中，AB＝BC＝2，D为BC的中点，在AC边上存在一点E，连结ED，EB，则△BDE周长的最小值为.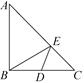
三、解答题
-
19. 如图，AB与CB是两条公路，C，D是两个村庄，现在要建一个菜市场，使它到两个村庄的距离相等，而且还要使它到两条公路的距离也相等，用尺规作图画出菜市场的位置.(不写作法，保留作图痕迹)
20. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．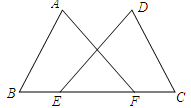
21. 如图，在等边△ABC中，BD＝CE，AD与BE相交于点P.求证：∠APE＝60°.
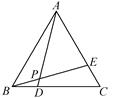22. 如图，∠ABC＝∠ADC＝90°，E是AC的中点，连结BD，DE，BE，EF⊥BD于点F. 求证：DF＝FB.
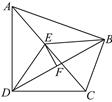23. 如图，把一张长方形纸片ABCD折叠起来，使其对角顶点A与C重合，若长方形的长BC为8，宽AB为4，求折叠后重叠部分的面积.
24. 如图，已知线段 与 相交于点 ，联结 ， 为 的中点， 为 的中点，联结 .若∠A=∠D，∠OEF=∠OFE，求证：AB=DC.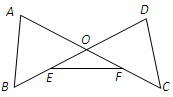
25. 如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
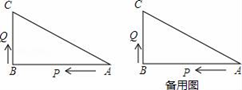(1)、出发2秒后，求PQ的长；(2)、当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．