浙江省杭州市三校2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-08-05 类型：期中考试
一、单选题
-
1. 在以下节水、节能、回收、绿色食品四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各组数中，不能作为直角三角形三边长的是（ ）A、1.5，2，3 B、5，12，13 C、7，24，25 D、8，15，173. 能说明命题“对于任何实数a，|a|＞﹣a”是假命题的一个反例可以是（ ）A、a＝﹣2 B、a＝ C、a＝1 D、a＝4. 如图，△ABC中，∠C＝80°，若沿图中虚线截去∠C，则∠1+∠2＝（ ）
A、360° B、260° C、180° D、140°5. 已知等腰△ABC的周长为18 cm，BC＝8 cm，若△ABC与△A′B′C′全等，则△A′B′C′的腰长等于（ ）．
A、8 cm B、2 cm或8 cm C、5 cm D、8 cm或5 cm6. 如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（ ）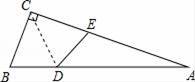
A、44° B、60° C、67° D、77°7. 在△ABC中，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是（ ）
A、5 B、6 C、4 D、4.88. 如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于点E.如果∠BAC=60°，∠ACE=24°，那么∠BCE的大小是（ ）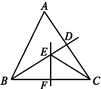
A、24° B、30° C、32° D、36°9. 如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处.若BC＝8，BE＝2.则AB2﹣AC2的值为（ ）
A、4 B、6 C、10 D、1610. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形.如图所示，如果大正方形的面积是100，小正方形的面积为20，那么每个直角三角形的周长为（ ）
A、 10+ B、10+ C、10+ D、24二、填空题
-
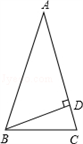
11. 如图，△ABC中，AB=AC，∠A=36°，BD是AC边上的高，则∠DBC的度数是.
12. Rt△ABC中，斜边BC＝3，则AB2+BC2+CA2的值为.13. 命题“等腰三角形的两个底角相等．”的逆命题是 ．14. 如图，△ABC中，D为AB的中点，BE⊥AC，垂足为E.若DE＝4，AE＝6，则BE的长度是.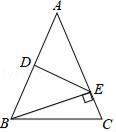
15. 平面上有△ACD与△BCE，其中AD与BE相交于P点，如图，若AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，则∠BPD的度数为.
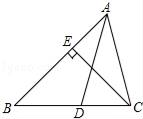
16. 小华是一位善于思考的学生，在一次数学活动课上，他将一副直角三角板如图位置摆放，A，B，D在同一直线上，EF∥AD，∠CAB＝∠EDF＝90°，∠C＝45°，∠E＝60°，量得DE＝2 .则BD＝.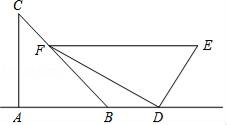
17. 如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC=°.
三、解答题
-
18. 如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝45°，求∠ADB的度数.
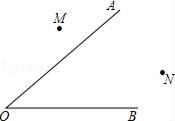
19. 请你用直尺和圆规作图（要求：不必写作法，但要保留作图痕迹）.已知：∠AOB，点M、N.求作：点P，使点P到OA、OB的距离相等，且PM＝PN.
20. 如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE.求证：△ACD≌△CBE.
21. 如图①是一个直角三角形纸片，∠C＝90°，AB＝13cm，BC＝5cm，将其折叠，使点C落在斜边上的点C′处，折痕为BD（如图②），求DC的长.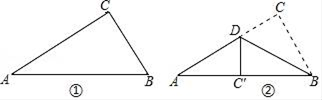
22. 如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高.
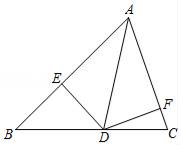(1)、求证AE＝AF.(2)、若AB+AC＝16，S△ABC＝24，∠EDF＝120°，求AD的长.23. 在△ABC中，AB＝AC，∠BAC＝90°，点D为AC上一动点.
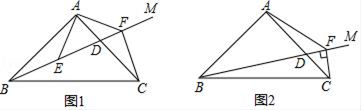(1)、如图1，点E、点F均是射线BD上的点并且满足AE＝AF，∠EAF＝90°.求证：△ABE≌△ACF；(2)、在（1）的条件下，求证：CF⊥BD；(3)、由（1）我们知道∠AFB＝45°，如图2，当点D的位置发生变化时，过点C作CF⊥BD于F，连接AF.那么∠AFB的度数是否发生变化？请证明你的结论.