广西南宁市2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-08-05 类型:期中考试
一、单选题
-
1. 下面有4个图案,其中有( )个是轴对称图形.
 A、一个 B、二个 C、三个 D、四个2. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A、一个 B、二个 C、三个 D、四个2. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )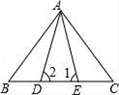 A、AB=AC B、∠BAE=∠CAD C、BE=DC D、AD=DE3. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
A、AB=AC B、∠BAE=∠CAD C、BE=DC D、AD=DE3. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )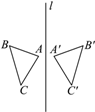 A、48° B、54° C、74° D、78°4. 一个等腰三角形的两边长分别是4和9,则它的周长是( )A、22 B、17 C、13 D、17或225. 如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A、48° B、54° C、74° D、78°4. 一个等腰三角形的两边长分别是4和9,则它的周长是( )A、22 B、17 C、13 D、17或225. 如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )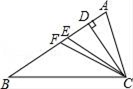 A、AB=2BF B、∠ACE= ∠ACB C、AE=BE D、CD⊥BE6. 到三角形三个顶点的距离相等的点是三角形( )的交点.A、三个内角平分线 B、三边垂直平分线 C、三条中线 D、三条高7. 如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
A、AB=2BF B、∠ACE= ∠ACB C、AE=BE D、CD⊥BE6. 到三角形三个顶点的距离相等的点是三角形( )的交点.A、三个内角平分线 B、三边垂直平分线 C、三条中线 D、三条高7. 如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( ) A、AB=DE B、DF∥AC C、∠E=∠ABC D、AB∥DE8. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A、AB=DE B、DF∥AC C、∠E=∠ABC D、AB∥DE8. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( ) A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD9. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.则这四个结论中正确的有( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD9. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.则这四个结论中正确的有( )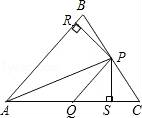 A、4个 B、3个 C、2个 D、1个10. 等腰三角形的一个角是50°,则它的底角是( )A、50° B、50°或65° C、80° D、65°11. 如图,在射线OA,OB上分别截取OA1=OB1 , 连接A1B1 , 在B1A1 , B1B上分别截取B1A2=B1B2 , 连接A2B2 , …按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
A、4个 B、3个 C、2个 D、1个10. 等腰三角形的一个角是50°,则它的底角是( )A、50° B、50°或65° C、80° D、65°11. 如图,在射线OA,OB上分别截取OA1=OB1 , 连接A1B1 , 在B1A1 , B1B上分别截取B1A2=B1B2 , 连接A2B2 , …按此规律作下去,若∠A1B1O=α,则∠A10B10O=( ) A、 B、 C、 D、12. 平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )A、4个 B、8个 C、10个 D、12个
A、 B、 C、 D、12. 平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )A、4个 B、8个 C、10个 D、12个二、填空题
-
13. 从一个十二边形的同一个顶点出发,分别连接这个顶点与其余各点,可以把这个多边形分割成个三角形.14. 如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN= .
 15. 在△ABC中,∠C=30°,∠A-∠B=30°,则∠A=.16. 等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为 .17. 已知点P(﹣2,1),则点P关于x轴对称的点的坐标是 .18. 如图,AD是△ABC的角平分线,AB:AC=3:2,△ABD的面积为15,则△ACD的面积为.
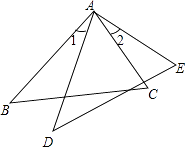
15. 在△ABC中,∠C=30°,∠A-∠B=30°,则∠A=.16. 等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为 .17. 已知点P(﹣2,1),则点P关于x轴对称的点的坐标是 .18. 如图,AD是△ABC的角平分线,AB:AC=3:2,△ABD的面积为15,则△ACD的面积为.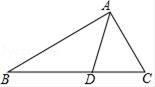 19. ∠A+∠B+∠C+∠D+∠E+∠F的度数=.
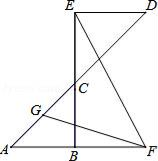
19. ∠A+∠B+∠C+∠D+∠E+∠F的度数=. 20. 如图,△ABC中,AB=63,AC=50,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为.
20. 如图,△ABC中,AB=63,AC=50,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为.
三、解答题
-
21. 一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.22. 如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线.
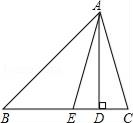 (1)、若∠B=38°,∠C=70°,求∠DAE的度数;(2)、若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.23. 如图.在△ABC中,AD是角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.
(1)、若∠B=38°,∠C=70°,求∠DAE的度数;(2)、若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.23. 如图.在△ABC中,AD是角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.求证:EB=FC.