浙江省温州市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 在直角坐标系中,点A(-6,5)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 不等式x+1<2的解为( )A、 B、 C、 D、3. 直线y=-2x+6与x轴的交点坐标是( )A、 B、 C、 D、4. 一副三角板按如图所示方式叠放在一起,则图中∠α等于( )
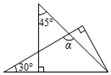 A、 B、 C、 D、5. 下列选项中a的值,可以作为命题“a2>4,则a>2”是假命题的反例是( )A、 B、 C、 D、6. 下列选项中的尺规作图,能推出PA=PC的是( )A、
A、 B、 C、 D、5. 下列选项中a的值,可以作为命题“a2>4,则a>2”是假命题的反例是( )A、 B、 C、 D、6. 下列选项中的尺规作图,能推出PA=PC的是( )A、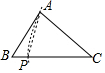 B、
B、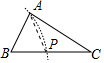 C、
C、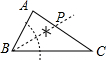 D、
D、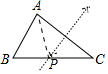 7. 如图,将点P(-1,3)向右平移n个单位后落在直线y=2x-1上的点P′处,则n等于( )
7. 如图,将点P(-1,3)向右平移n个单位后落在直线y=2x-1上的点P′处,则n等于( )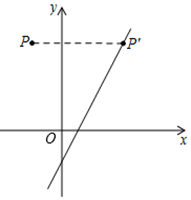 A、2 B、 C、3 D、48. 如图,在△ABC中,AB=AC=6,点D在边AC上,AD的中垂线交BC于点E.若∠AED=∠B,CE=3BE,则CD等于( )
A、2 B、 C、3 D、48. 如图,在△ABC中,AB=AC=6,点D在边AC上,AD的中垂线交BC于点E.若∠AED=∠B,CE=3BE,则CD等于( )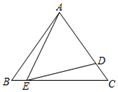 A、 B、2 C、 D、39. 如图,在等腰△OAB中,∠OAB=90°,点A在x轴正半轴上,点B在第一象限,以AB为斜边向右侧作等腰Rt△ABC,则直线OC的函数表达式为( )
A、 B、2 C、 D、39. 如图,在等腰△OAB中,∠OAB=90°,点A在x轴正半轴上,点B在第一象限,以AB为斜边向右侧作等腰Rt△ABC,则直线OC的函数表达式为( )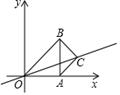 A、 B、 C、 D、10. 如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B→A→D→C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
A、 B、 C、 D、10. 如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B→A→D→C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )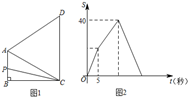 A、10 B、 C、8 D、
A、10 B、 C、8 D、二、填空题
-
11. 若2a<2b,则ab.(填“>”或“=”或“<”)12. 点 关于x轴的对称点的坐标是.13. 设等腰三角形的底角为x度,顶角为y度,则y关于x的函数表达式为.14. “a的2倍与b的和是正数”用不等式表示为.15. 已知y是关于x的一次函数,下表列出了部分对应值,则m的值为.
x
0
3
4
y
20
m
8
16. 如图,直线y=- x+ 交x轴于点A,交y轴于点B,点C在第一象限内,若△ABC是等边三角形,则点C的坐标为.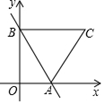 17. 如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为 ,四边形BCPD的周长为12+ ,则BC等于.
17. 如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为 ,四边形BCPD的周长为12+ ,则BC等于. 18. 如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则阴影部分面积为 .
18. 如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则阴影部分面积为 .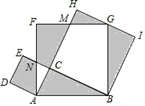
三、解答题
-
19. 解不等式组 ,并把解表示在数轴上.
 20. 如图,点A,F,C,D在同一条直线上,EF∥BC,AB∥DE,AB=DE,求证:AF=CD.
20. 如图,点A,F,C,D在同一条直线上,EF∥BC,AB∥DE,AB=DE,求证:AF=CD. 21. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形,如图,已知整点A(2,2),B(4,1),请在所给网格区域(含边界)上按要求画整点三角形.
21. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形,如图,已知整点A(2,2),B(4,1),请在所给网格区域(含边界)上按要求画整点三角形.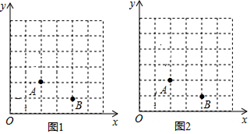 (1)、在图1中画一个等腰△PAB,使点P的横坐标大于点A的横坐标.(2)、在图2中画一个直角△PAB,使点P的横坐标等于点P,B的纵坐标之和.22. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)、在图1中画一个等腰△PAB,使点P的横坐标大于点A的横坐标.(2)、在图2中画一个直角△PAB,使点P的横坐标等于点P,B的纵坐标之和.22. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E. (1)、求证:∠AEC=∠ACE;(2)、若∠AEC=2∠B,AD=2,求AB的长.23. 某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.(1)、求y关于x的函数表达式.(2)、若购进A种的数量不少于B种的数量.
(1)、求证:∠AEC=∠ACE;(2)、若∠AEC=2∠B,AD=2,求AB的长.23. 某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.(1)、求y关于x的函数表达式.(2)、若购进A种的数量不少于B种的数量.①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有本(直接写出答案)
24. 如图,直线y=kx+8(k<0)交y轴于点A,交x轴于点B.将△AOB关于直线AB翻折得到△APB.过点A作AC∥x轴交线段BP于点C,在AC上取点D,且点D在点C的右侧,连结BD.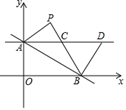 (1)、求证:AC=BC(2)、若AC=10.
(1)、求证:AC=BC(2)、若AC=10.①求直线AB的表达式.
②若△BCD是以BC为腰的等腰三角形,求AD的长.
(3)、若BD平分∠OBP的外角,记△APC面积为S1 , △BCD面积为S2 , 且 = ,则 的值为(直接写出答案)