浙江省绍兴市诸暨市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 下列表示天气符号的图形中,不是轴对称图形的是( )A、
 冰雹
B、
冰雹
B、 雷阵雨
C、
雷阵雨
C、 晴
D、
晴
D、 大雪
2. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )A、1,2,3 B、1,2,4 C、2,3,4 D、2,2,43. 在平面直角坐标系中,点P(3,2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若 ,则下列式子中正确的是( )A、 B、 C、 D、5. 如图,点P在BC上, 于点B, 于点C, ≌ ,其中BP=CD,则下列结论中错误是( )
大雪
2. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )A、1,2,3 B、1,2,4 C、2,3,4 D、2,2,43. 在平面直角坐标系中,点P(3,2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若 ,则下列式子中正确的是( )A、 B、 C、 D、5. 如图,点P在BC上, 于点B, 于点C, ≌ ,其中BP=CD,则下列结论中错误是( )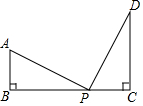 A、 B、 C、 D、6. 已知一个等腰三角形一内角的度数为 ,则这个等腰三角形顶角的度数为( )A、 B、 C、 或 D、 或7. 某市为了鼓励节约用水,按以下规定收水费: 每户每月用水量不超过 ,则每立方米水费为 元, 每户用水量超过 ,则超过的部分每立方米水费2元,设某户一个月所交水费为 元 ,用水量为 ,则y与x的函数关系用图象表示为( )A、
A、 B、 C、 D、6. 已知一个等腰三角形一内角的度数为 ,则这个等腰三角形顶角的度数为( )A、 B、 C、 或 D、 或7. 某市为了鼓励节约用水,按以下规定收水费: 每户每月用水量不超过 ,则每立方米水费为 元, 每户用水量超过 ,则超过的部分每立方米水费2元,设某户一个月所交水费为 元 ,用水量为 ,则y与x的函数关系用图象表示为( )A、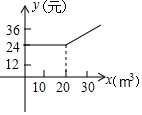 B、
B、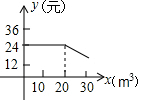 C、
C、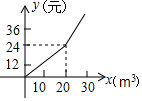 D、
D、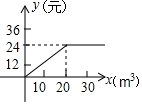 8. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图折叠,使点A与点B重合,则折痕DE的长是( )
8. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图折叠,使点A与点B重合,则折痕DE的长是( )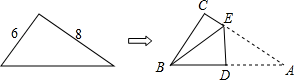 A、 B、 C、 D、9. 如图A所示,将长为20cm,宽为2cm的长方形白纸条,折成图B所示的图形并在其一面着色,则着色部分的面积为( )
A、 B、 C、 D、9. 如图A所示,将长为20cm,宽为2cm的长方形白纸条,折成图B所示的图形并在其一面着色,则着色部分的面积为( )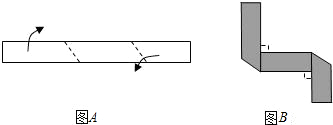 A、 B、 C、 D、10. 已知 ,则直线 一定经过的象限是( )A、第一、三、四象限 B、第一、二、四象限 C、第一、四象限 D、第二、三象限
A、 B、 C、 D、10. 已知 ,则直线 一定经过的象限是( )A、第一、三、四象限 B、第一、二、四象限 C、第一、四象限 D、第二、三象限二、填空题
-
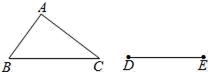
11. 在Rt△ABC中,∠C=90°,∠A=70°,则∠B= .12. 将点 向右平移2个单位长度得到点B的坐标是 .13. 请写出一个图象经过点 的一次函数的表达式: .14. 一个直角三角形的两条直角边长分别为3,4,则第三边为 .15. 在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对题.16. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.
 17. 如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
17. 如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .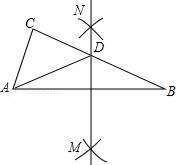 18. 如图钢架中,焊上等长的7根钢条来加固钢架,若 ,则 的度数是 .
18. 如图钢架中,焊上等长的7根钢条来加固钢架,若 ,则 的度数是 .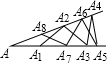 19. 现在全省各大景区都在流行“真人CS“娱乐项目,其中有一个“快速抢点”游戏,游戏规则:如图,用绳子围成的一个边长为10m的正方形ABCD场地中,游戏者从AB边上的点E处出发,分别先后赶往边BC、CD、DA上插小旗子,最后回到点 已知 ,则游戏者所跑的最少路程是多少
19. 现在全省各大景区都在流行“真人CS“娱乐项目,其中有一个“快速抢点”游戏,游戏规则:如图,用绳子围成的一个边长为10m的正方形ABCD场地中,游戏者从AB边上的点E处出发,分别先后赶往边BC、CD、DA上插小旗子,最后回到点 已知 ,则游戏者所跑的最少路程是多少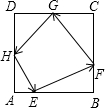
三、解答题
-
20. 在如图所示的正方形网格中,每个小正方形的边长
为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为( ,5),( ,3).
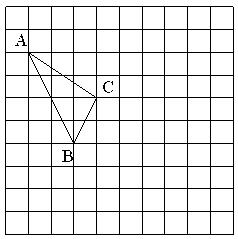 (1)、请在如图所示的网格平面内作出平面直角坐标系;
(1)、请在如图所示的网格平面内作出平面直角坐标系;
(2)、请作出△ABC关于y轴对称的△A′B′C′;
(3)、写出点B′的坐标.
21. 解下列不等式 组 :(1)、2x+1<x+5;(2)、22. 如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.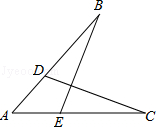 23. 已知直线 经过点 和 .
23. 已知直线 经过点 和 .
(1)、求该直线的函数表达式;
(2)、求该直线与x轴,y轴的交点坐标.
24. 如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm.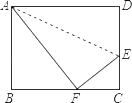 (1)、求线段BF的长;(2)、求△AEF的面积.25. 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣ x+b过点C.
(1)、求线段BF的长;(2)、求△AEF的面积.25. 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣ x+b过点C.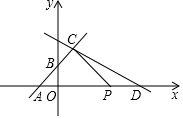 (1)、求m和b的值;(2)、直线y=﹣ x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动.设点P的运动时间为t秒.
(1)、求m和b的值;(2)、直线y=﹣ x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动.设点P的运动时间为t秒.①若点P在线段DA上,且△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.