浙江省绍兴市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 下列各组数不可能是一个三角形的边长的是( )A、7,8,9 B、5,6,7 C、3,4,5 D、1,2,32. 满足-1<x≤2的数在数轴上表示为( ).A、
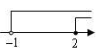 B、
B、 C、
C、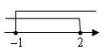 D、
D、 3. 在一个直角三角形中,有一个锐角等于 ,则另一个锐角的度数是( )A、 B、 C、 D、4. 已知正比例函数的图象经过点 ,则这个正比例函数的表达式为( )A、 B、 C、 D、5. 如图 , ,要使 ≌ ,需要添加下列选项中的( )
3. 在一个直角三角形中,有一个锐角等于 ,则另一个锐角的度数是( )A、 B、 C、 D、4. 已知正比例函数的图象经过点 ,则这个正比例函数的表达式为( )A、 B、 C、 D、5. 如图 , ,要使 ≌ ,需要添加下列选项中的( ) A、 B、 C、 D、6. 一次函数 的图象经过坐标系的( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限7. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( )
A、 B、 C、 D、6. 一次函数 的图象经过坐标系的( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限7. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( ) A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小8. 如图, ≌ , ,点A,D,E在同一条直线上, ,则 的度数是( )
A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小8. 如图, ≌ , ,点A,D,E在同一条直线上, ,则 的度数是( ) A、 B、 C、 D、9. 在平面直角坐标系中,已知 、 ,若要在x轴上找一点P,使 最短,则点P的坐标为( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,点A的坐标为 ,以线段OA为边在第四象限内作等边 ,点C为x轴正半轴上一动点 ,连接BC,以线段BC为边在第四象限内作等边 ,直线DA交y轴于点E,点E的坐标是( )
A、 B、 C、 D、9. 在平面直角坐标系中,已知 、 ,若要在x轴上找一点P,使 最短,则点P的坐标为( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,点A的坐标为 ,以线段OA为边在第四象限内作等边 ,点C为x轴正半轴上一动点 ,连接BC,以线段BC为边在第四象限内作等边 ,直线DA交y轴于点E,点E的坐标是( )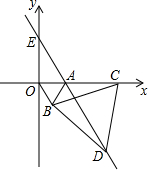 A、点E的坐标随着点C位置的变化而变化 B、 C、 D、
A、点E的坐标随着点C位置的变化而变化 B、 C、 D、二、填空题
-
11. 命题“两直线平行,同位角相等”的逆命题是。12. 等腰三角形ABC中顶角 ,底角 的度数是.13. 不等式 的负整数解为.14. 在平面直角坐标系中,点(2,3)到x轴的距离是.15. 如图是一次函数的y=kx+b图象,则关于x的不等式kx+b>0的解集为.
 16. 定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转 角度,这样的图形运动叫作图形的 变换 如图,等边 的边长为1,点A在第一象限,点B与原点0重合,点C在x轴的正半轴上 就是 经 变换后所得的图形,则点 的坐标是.
16. 定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转 角度,这样的图形运动叫作图形的 变换 如图,等边 的边长为1,点A在第一象限,点B与原点0重合,点C在x轴的正半轴上 就是 经 变换后所得的图形,则点 的坐标是.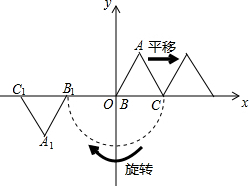 17. 如图,我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是20,小正方形的面积是8,直角三角形的两直角边分别是a和b,那么ab的值为.
17. 如图,我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是20,小正方形的面积是8,直角三角形的两直角边分别是a和b,那么ab的值为. 18. 如图, 中, ,D在BC上,E为AB中点,AD、CE相交于F, 若 ,则 等于
18. 如图, 中, ,D在BC上,E为AB中点,AD、CE相交于F, 若 ,则 等于
三、解答题
-
19. 解不等式 组)(1)、(2)、20. 如图, 中, ,D是BC中点, 求BC的长.
 21. 一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量 (升)关于加满油后已行驶的路程 (千米)的函数图象.
21. 一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量 (升)关于加满油后已行驶的路程 (千米)的函数图象.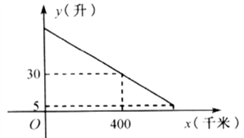 (1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.22. “绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
(1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.22. “绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:路程(千米)
甲仓库
乙仓库
A果园
15
25
B果园
20
20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元,
(1)、根据题意,填写下表.(温馨提示:请填写在答题卷相对应的表格内)运量(吨)
运费(元)
甲仓库
乙仓库
甲仓库
乙仓库
A果园
x
110﹣x
2×15x
2×25(110﹣x)
B果园
(2)、设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?23. 小敏思考解决如下问题:原题:如图1,四边形ABCD中 , , 点P,Q分别在四边形ABCD的边BC,CD上, ,求证: .
 (1)、 ;(2)、小敏进行探索,如图2,将点P,Q的位置特殊化,使 , ,点E,F分别在边BC,CD上,此时她证明了 请你证明此时结论;(3)、受以上 的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为E,F,请你继续完成原题的证明.24. 点O为平面直角坐标系的坐标原点,直线 与x轴相交于点A,与y轴相交于点B.(1)、求点A,点B的坐标;(2)、若 ∠BAO=∠AOC ,求直线OC的函数表达式;
(1)、 ;(2)、小敏进行探索,如图2,将点P,Q的位置特殊化,使 , ,点E,F分别在边BC,CD上,此时她证明了 请你证明此时结论;(3)、受以上 的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为E,F,请你继续完成原题的证明.24. 点O为平面直角坐标系的坐标原点,直线 与x轴相交于点A,与y轴相交于点B.(1)、求点A,点B的坐标;(2)、若 ∠BAO=∠AOC ,求直线OC的函数表达式;
(3)、点D是直线 上的一点,把线段BD绕点D旋转 ,点B的对应点为点 若点E恰好落在直线AB上,则称这样的点D为“好点”,求出所有“好点”D的坐标.